


Inicio Unidad I Unidad II Unidad III Unidad IV Unidad V Bibliografía

Diseña circuitos combinacionales utilizados en los sistemas computacionales mediante la identificación de las características básicas de los circuitos combinacionales y circuitos integrados TTL y CMOS y el empleo de compuertas lógicas integradas en los CI.
En esta unidad encontrarás los siguientes temas:
3.1 Circuitos combinacionales.
3.1.1 Circuitos combinacionales de 2 etapas.
3.2 Compuertas lógicas integradas.
3.2.1 Codificadores y decodificadores.
3.2.2 Multiplexores y demultiplexores.
3.3 Introducción a los módulos aritméticos.
3.3.1 Medio sumador y sumador completo.
3.3.2 Unidad aritméticas lógica (ALU).
3.4 Familias lógicas TTL y CMOS.
3.5 Funciones Booleanas empleando CI.
A los circuitos digitales que se conforman con entradas, salidas y se implementan con compuertas lógicas, para realizar una función específica y que esta no requiere de almacenamiento, se les llama Circuitos combinacionales. En estos circuitos la salida depende exclusivamente del valor de las entradas. Lo explicaremos con ejemplos:
Ejemplo 1.- Que funciones realiza este circuito de la figura 33
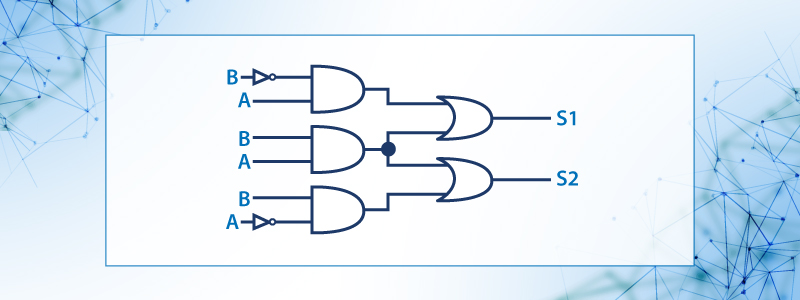
Figura 23. Diagrama esquemático de las compuertas NOT, AND, OR, NAND y NOR
Solución:
Para entender que hace este circuito, obtengamos la función que realiza:
Se observa que los miniterminos (m5 , m7 ) y (m6 , m7) se pueden factorizar, para sacar provecho de que tienen términos con variables complementarias, esto es m5 tiene a G y m7 tiene a G’ lo mismo para m6 y m7 que tienen a L y L’ respectivamente.
Podemos ver que S1=B’A + BA y S2=BA’ + BA
Para analizar lo que hace esta función para S1 y S2 nos apoyaremos en una TABLA DE VERDAD figura 34
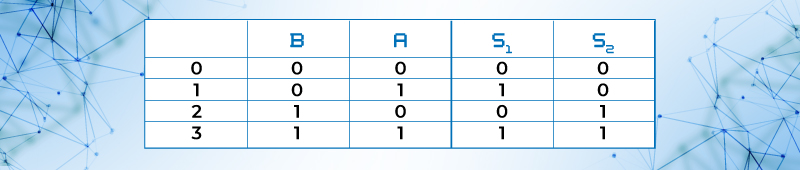
Tabla 20. TABLA DE VERDAD para S1 y S2.
que la construiremos usando LÓGICA POSITIVA, esto es, para cuando tenemos B = 1, B’ = 0, los valores que corresponden a cada variable se asignan en forma vertical, las ENTRADAS son las variables B, A y las SALIDAS son S1 y S2 , para las entradas se ponen las posibles combinaciones que se pueden dar para B y A, la forma fácil es poner para la primera variable A, los valores de 0 1 0 1, como ya se dijo en forma vertical, para la segunda variable B serán 0 0 1 1 y para las variables de salida S1 y S2 los valores que estas adquieren ya sea 0 o 1 según sea la combinación de entrada deseada, quedando la tabla de verdad de la siguiente forma. Nótese que se le asignaron los valores de 0,1,2,y 3 a las filas que representan esta combinación en número binario según la fila que corresponda, a estos valores se les llama miniterminos o suma de productos en razón a que los miniterminos se pueden representar de la manera siguiente: mo = B’A’, m1= B’Á, m2 = BA’ y m3 = BA por lo que al definir la función, queda para:
S1 = {1, 3} y para S2 = {2,3}
Lo mismo, pero con las variables de entrada para mostrar los miniterminos
S1 = B’A + BA y para S2 = BA’ + BA
m1 m3 m2 m3
lo que hace esta función, es, para que el valor de S1 sea 1 es si y sólo si el m1 = 1 o si el m3 = 1 y para que S2 = 1 si y sólo si el m2 = 1 o si el m3 = 1.
Dicho lo mismo, pero con otras palabras el Led conectado a la salida de S1 prende si y sólo si la entrada es 1 o 3 en número binario y S2 tendrá el Led conectado prendido si y sólo si la entrada es 2 o 3 en número binario
En resumen, entendemos que los valores en las columnas a la izquierda de la TABLA DE VERDAD son entradas y los valores en las columnas a la derecha son salidas o funciones de salida, y para las filas estas representan el minitermino en forma de suma de productos asignadas con el número binario que corresponde. Y las funciones de salida se les asignan los miniterminos que están en la misma fila en que la función de salida vale 1, según sea el caso.
Diseño de un circuito combinacional
Para diseñar un circuito combinacional es requisito que su salida o funciones de salida a ser 1 solo dependen del valor de entrada en la fila que corresponda y que esta salida no requiera de almacenamiento alguno.
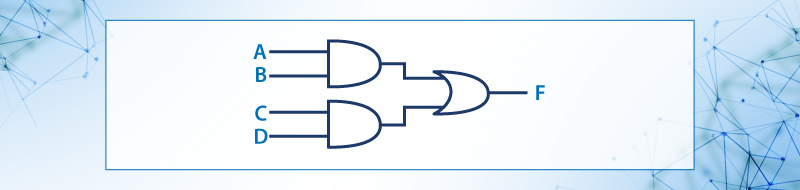
Figura 24. Circuito Combinacional.
Para explicar el diseño de circuitos combinacionales lo haremos con ejemplos
Ejemplo 2.- Diseñar un circuito digital que permita sonar una alarma en el caso siguiente:
En una granja, se tiene un gallinero, un perro que a veces anda suelto y un almacén en donde se guardan las semillas con que se alimenta a todos los animales de la granja, se requiere una alarma de luz y sonido que se active en caso de peligro, ya sea porque el perro esta suelto y las gallinas afuera del gallinero o porque el almacén está abierto, las gallinas sueltas y esta se pueden comer las semillas (Asumir que se tienen los sensores adecuados).
SOLUCIÓN. -
1.- Establecemos lo siguiente.
G = gallinas P = perro A = almacén
En donde:
G = 1 SI gallinas sueltas G = 0 NO gallinas sueltas
P = 1 SI perro suelto P = 0 NO perro suelto
A = 1 SI almacén abierto A = 0 No almacén abierto
2.- Se realiza una TABLA DE VERDAD que represente el problema.
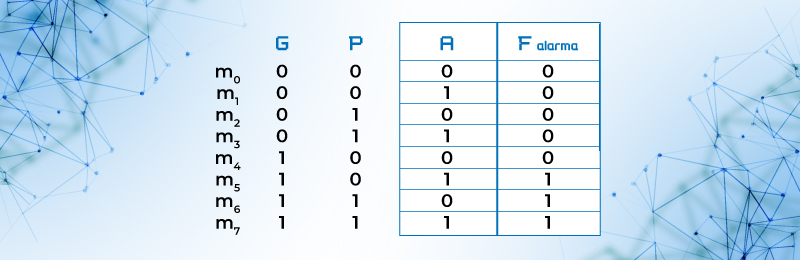
Tabla 21. Tabla de verdad para representar el problema del granjero
3.- Obtener las funciones de salida.
Por lo tanto Falarma = m5 + m6 + m7 = { 5, 6, 7} = GP’A + GPA’ + GPA
4.- Dibujar el circuito.
La tabla de verdad la reducimos por mapas de Karnaugh Figura 36 lo que da el circuito digital de la figura 37 y con esto se concluye el diseño.
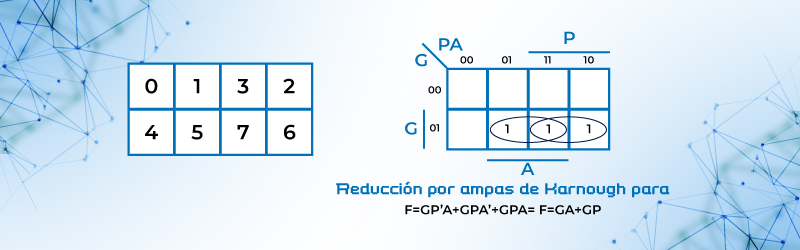
Figura 25. Reducción por mapas de Karnaugh.
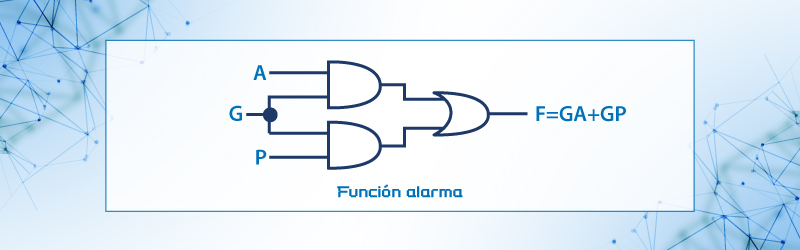
Figura 26. Circuito para la función alarma F=GA+GP.
Aunque se haya terminado el diseño, para aprender más, es conveniente realizar los siguientes dos pasos:
5.- Realizar con un simulador el circuito.
El Hacer este punto nos permite verificar si el diseño realiza las funciones que deseamos.
6.- Elaborar físicamente el circuito
Al construir el circuito habremos terminado completamente el diseño
Ejemplo 3.- Se tiene varios espacios para usar como almacén, pero no se tiene acceso visual para poder saber qué tipo de tanque se puede almacenar, si el que ocupa un lugar sencillo o el que ocupa doble, por lo que se pide: Diseñar un circuito que permita indicar con led´s en un tablero la posición en que se puede almacenar la mercancía en el caso siguiente:
SOLUCIÓN. -
1.- Establecemos lo siguiente.
Q = tanque tipo Q
Q = 1 Si almacenar tanque Q
Q = 0 NO almacenar tanque Q
A= sensor en espacio A B= sensor en espacio B C= sensor en espacio C D= sensor en espacio D
A=1 ocupado B=1 ocupado C = 1 ocupado D = 1 ocupado
A=0 vacío B = 0 vacío C = 0 vacío D = 0 vacío
2.- Realizar la TABLA DE VERDAD que represente la solución al problema.
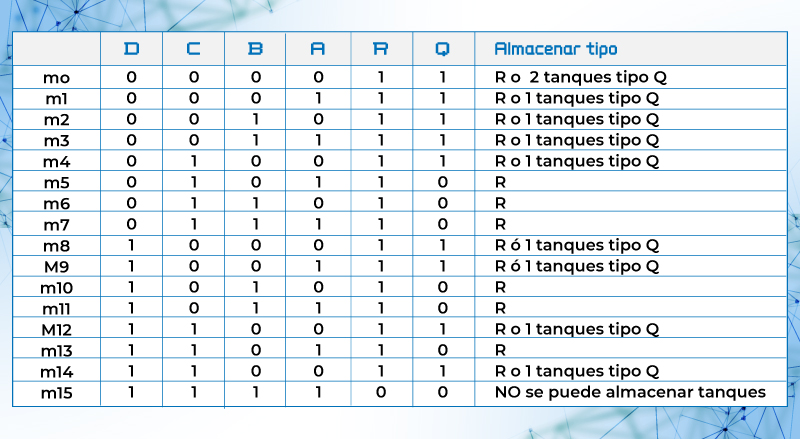
Tabla 22. Tabla de verdad para problema de almacenamiento
3.- Obtener las funciones de salida.
R = M´15 = M15 Negada ={15}´= (DCBA)´
Q = M0 + M1 + M2 + M3 + M4 + M8 + M9 + M12 + M14
= {0,1,2,3,4,8,9,12,14}
= D´C´B´A´ + D´C´B´A + D´C´BA´+ D´CB´A´ + DC´B´A´ + DCB’ A´ + DC´B´A + DCBA + DCBA´
Reducir por mapas de karnaugh
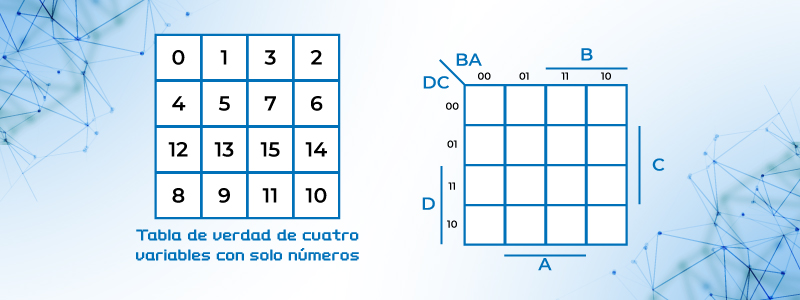
Figura 27. Mapa de Karnaugh de 4 variables.
Hacer la reducción y hacer el diagrama esquemático del circuito digital
5.- Realizar con un simulador el circuito.
El hacer este punto nos permite verificar si el diseño realiza las funciones que deseamos.
6.- Elaborar físicamente el circuito
Al construir el circuito habremos terminado completamente el diseño.
Etapa de un circuito lógico se le llama al conjunto de circuitos que tienen el mismo orden de entrada, es decir primera entrada, segunda entrada, etc. Luego entonces un circuito lógico de 2 etapas es un circuito muy simple pues solo se contempla la formación de señales lógicas en dos momentos.
El analizar una circuito lógico tiene como propósito obtener el conjunto de funciones lógicas o ecuaciones que describen las operaciones booleanas que lleva a cabo el circuito, esto lo explicaremos con el siguiente ejemplo.
Ejemplo 4.- Analizar el circuito lógico mostrado y describir las funciones lógicas o ecuaciones que describen las operaciones booleanas que se llevan a cabo en cada etapa para dar las salidas S y C
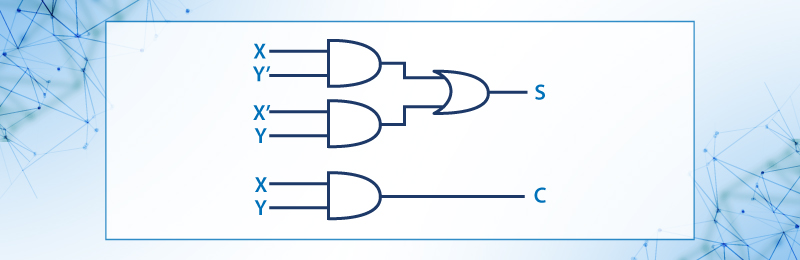
Figura 28. Circuito lógico para el ejemplo 49
Solución En la primera etapa se tienen solo compuertas AND, en la parte superior tenemos ´dos compuerta una para xy’ y otra para x’y para la tercera AND compuerta xy finalmente en la segunda etapa solo la compuerta OR, en la que tenemos (xy’ + x’y) = S
Para C tendremos C = xy que como ya se dijo es de una sola etapa.

