Unidad de competencia:

Simplificar funciones lógicas para el diseño de circuitos digitales aplicando el álgebra de Boole y los mapas de Karnaugh, diferenciando las compuertas lógicas y elaborando tablas de verdad.

El álgebra Booleana fue desarrollada por George Boole en 1854 mucho antes que se inventara los transistores, para realizar operaciones lógicas con variables de sólo dos valores “FALSO” y “VERDADERO”. En 1938 C.E. Shannon introdujo el uso de esta álgebra en la electrónica digital pues se manejan también variables con solo dos valores “0” y “1”.

2.1.1. Definición Axiomática del álgebra Booleana

Recordando que los postulados en un sistema matemático son los supuestos básicos a partir de los cuales es posible construir dicho sistema.

Se debe de tener presente el postulado de cerradura para una álgebra booleana que establece:

Si X,Y Є ( 0, 1) → X # Y Є ( 0, 1)

Que se lee:

Si X,Y tienen los valores de 0 o 1 entonces X operación Y también tiene valores entre 0 o 1

Por ejemplo 0 + 1 = 1, el operador de suma + es cerrada

No así el operador resta – , puesto que 0 – 1 = – 1 y este valor NO está entre (0,1)

Con esto se quiere decir que las operaciones con números booleanos o binarios siempre arrojará para cada función, variables con valores de 0 o 1.

Sea la función F = X + Y +Z será = 0 o 1 dependiendo de los valores de cada variable.

Postulados del Álgebra Booleana

1. a) Cerradura respecto al operador suma +

b) Cerradura respecto al operador multiplicación x,

Este operador también se representa ya sea por variables seguidas, una después de otra, por un punto • también por paréntesis ( ).

2. a) Existe un elemento identidad -Cero 0- respecto a la suma +, X + 0 = 0

b) Existencia de elemento identidad Uno 1 respecto a la multiplicación × , X × 1 = X

3. a) Conmutativa respecto a suma + X +Y = Y + X.

b) Conmutativa respecto a multiplicación × X Y = Y X.

4. a) La multiplicación × es distributiva respecto a la suma +, X (Y+Z) = (XY) + (XZ).

b) La suma + es distributiva respecto a la multiplicación × X+(YZ) = (X+Y)(X+Z).

5. Existe para X su complemento X’, tal que X + X’ = 1 y XX’ = 0

6. Por lo menos existen dos elementos X,Y Є ( 0, 1) tales que X ≠ Y.

Teoremas del Álgebra Booleana

Teorema 1       X + X = X       X × X = X

Teorema 2       X + 1 = X       X × 0 = 0

Teorema 3, involución       (X’)’ = X

Teorema 4, asociatividad       X + (Y + Z) = (X + Y) + Z       X(YZ) = (XY)Z

Teorema 5, De Morgan       (X + Y)’ = X’Y’       (XY)’ = X’ + Y’

Teorema 6, Absorción       X + XY = X       X(X + Y) = X

Demostración de los teoremas

Se pueden demostrar construyendo una tabla de verdad para lado de la igualdad, si son iguales, queda demostrado, esto es:

Ejemplo 20.- Para el teorema 5, De Morgan.

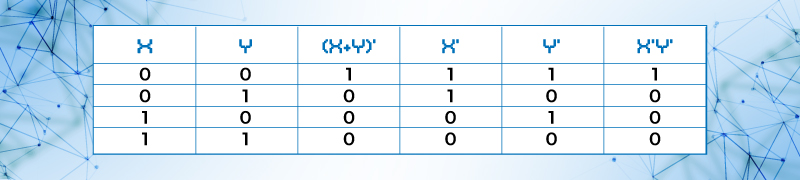
Tabla 6. Tabla de verdad que demuestra el teorema De Morgan

Otra manera de demostrar los teoremas es con el apoyo de los postulados, esto es: Demostrar el teorema 1 para la suma: X + X = X.

X + X = (X + X) •       postulado 2b)

= (X + X) • (X + X’)       5a)

= XX + XX’               4b)

= X + 0               5b)

= X               2a)

Actividad complementaria 1:

---

Demostrar los otros teoremas.

Existe en el álgebra booleana el principio de dualidad el cual consiste en que para encontrar el dual de algún postulado, se intercambian los operadores y se sustituyen los 0s por 1s y los 1s por 0’s:

Ejemplo 1.- para el postulado 2a) X + 1 = 1 Su dual es 2b) X • 0 = 0 o También X +0 =X y X•1=X

2.1.2. Funciones lógicas AND, OR, NOT

Operaciones binarias.

Las operaciones básicas que se realizan en el álgebra booleana son AND, OR, Y NOT, a partir de ellas se derivan todas demás. La operación que realizan se muestra con la tabla de verdad que es un listado sistemático de todas las posibles combinaciones de los valores 0s y 1s de las variables, incluyendo las entradas y las salidas.

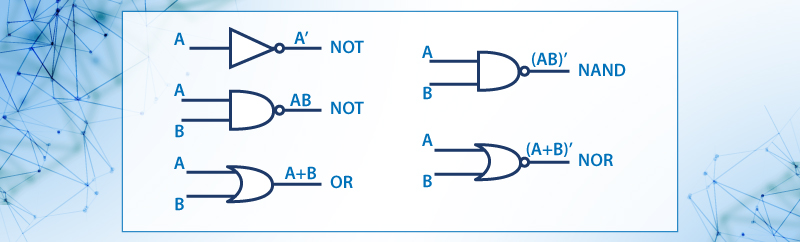
Figura 7. Diagrama esquemático de las compuertas NOT, AND, OR, NAND y NOR

Representación de las operaciones binarias con tablas de verdad.

Función AND

Tabla de verdad de la función B and A llamada función AND

También se esto se escribe función B and A = ByA = B•A = BA

Cabe señalar que la notación comúnmente empleada es AB.

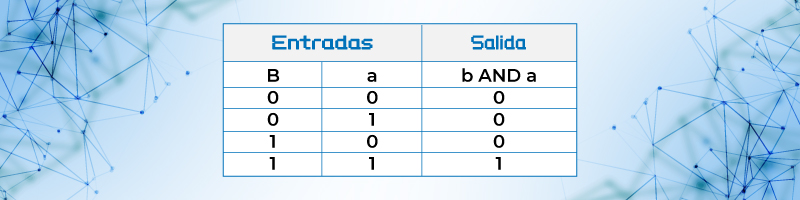
Tabla 7. Tabla de verdad de la función B and A llamada función AND

Función OR

Tabla de verdad de la función B or A llamada función OR También esto se escribe función B or A = B+A = B o´A La notación comúnmente usada A+B.

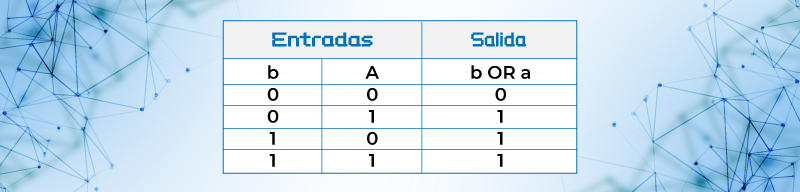
Tabla 8. Tabla de verdad de la función B or A llamada función OR

Función not A

Tabla de verdad de la función not A llamada función negación de A o también Fa= A’

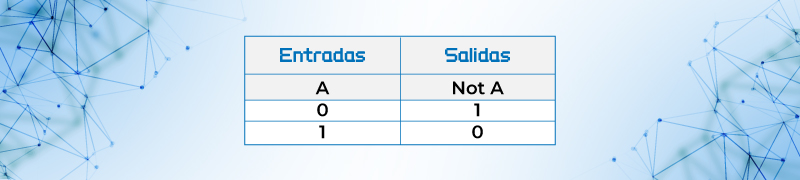
Tabla 9. Tabla de verdad de la función not A llamada función negación de A

Para estos apuntes se usa la notación de A’ para A negada, AB para A and B y A+B para A or B.

Actividad complementaria 2:

---

Implementar las tablas para las compuertas NAND y NOR

Es importante observar lo siguiente en la tabla de verdad: A cada línea de renglón se le llama minitermino, en cada tabla anterior podemos observar que cada línea representa un valor binario, esto es: En la figura x1 solo se tienen dos valores: renglón 0 y renglón 1 En la figura x2 y se tienen 4 renglones: renglón 0 0, renglón 0 1, renglón 1 0 y renglón 1 1 Llamándose respectivamente minitermino 0, minitermino 1, minitermino 2 y minitermino 3 Y que la tabla de verdad tiene tantos renglones o miniterminos como 2 elevado al número de variables de la función, abreviamos minitermino con la palabra Min.

Ejemplo 2.- La función OR

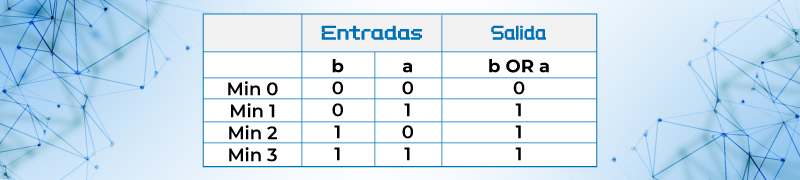
Tabla 10. Miniterminos de la función B or A, (FBorA), b+a

2.1.3. Forma canónica y estándar

Notación Canónica

Esto lo explicaremos con ejemplos:

Ejemplo 3.- Para la tabla x2 de la función AND, (FBA ) tenemos: FBA = { 3 } significa que para esta función solo el minitermino 3 tiene el valor binario de 1 de acuerdo con su tabla de verdad.

Para la tabla x3 de la función FBA= B or A, tenemos:

FBA = {1,2,3 } significa que para esta función los minit´rrmino 1,2,3 tiene el valor binario de 1, de acuerdo con su tabla de verdad. Otro ejemplo Determinar la tabla de verdad para la función FCBA ={0,3,5,6,7 } Solución.- La función FCBA indica que es una función con 3 variables: C; B; A esto significa que se tienen 23=8 minit´rrminos del 0 al 7

Notación estándar

Se explica con ejemplos

Ejemplo 4.- Escribir la función con todos sus valores de entrada en forma estándar:

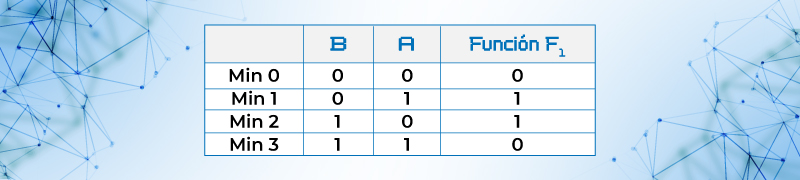
Tabla 11. Tabla de verdad función F1

Solución

Forma canónicas

F1= { 1.,2}

Forma estándar

F1= B’A + BA’

Ejemplo 5.- Escribir la función con todos sus valores de entrada en forma estándar:

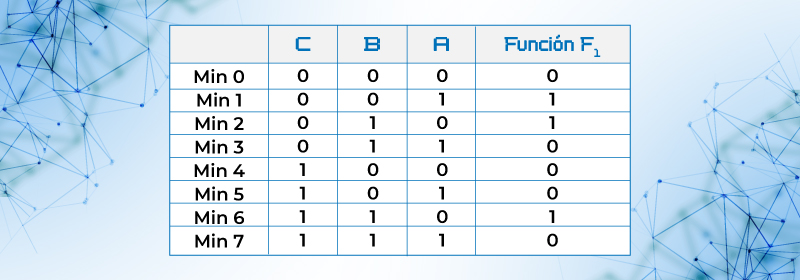
Tabla 12. Tabla de verdad función F2

Solución

Forma canónica

F2= { 1,.2 ,6}

Forma estándar

F2= C’B’A + C’BA’ + CBA’

Como se muestra en los ejemplos la forma estándar es escribir los Miniterminos correspondientes con valor de variable 1, con las letras que representan los valores de entrada.

En lo sucesivo no se indicará el minitermino respectivo en la tabla de verdad sino se dará por hecho.

Diagramas de Venn

La representación con diagramas de Venn es una ilustración gráfica en base a la teoría de conjuntos, su aplicación para compuertas lógicas como NOT, AND, OR NAND o NOR es sencilla, pero no resulta práctica en representaciones complejas por lo que no es muy común su uso. En el ejemplo 6 se muestran los esquemas de algunas aplicaciones.

Ejemplo 6.- Representación en diagramas de Venn de las operaciones binarias Q = XY + X y Q = X(Y+Z).

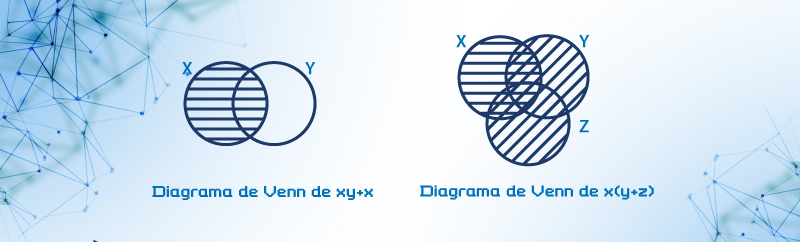
Figura 8. Diagramas de Venn

Expresiones a su forma estándar o no reducida

Para convertir una expresión a su forma estándar lo primero es ver qué valor es el que falta en cada parte de la expresión y cuáles son los valores utilizados en cada parte de ella, es decir que variables de entrada existen, completar la forma estándar es escribir la función con todas las variables.

Ejemplo 7.- Escribir en su forma estándar R= ABD+BC

En esta expresión para R los valores utilizados son ABCD, si la separamos podemos notar que a la primera parte le faltan valores C,C’, a la segunda le faltan los valores A,A’,D,D’. Por lo tanto, para expresar la función R en su forma estándar se multiplica cada minitermino por 1 en la forma (X+X’) para cada uno de los términos faltantes. Sumando todos los miniterminos y eliminando los que sean repetidos.

1. Primer minitermino.

ABD(1)= ABD(C+C’)= ABCD+ABC’D

2. Segundo minitérmino.

BC=(A+A’) BC (D+D’) = (ABC+A’BC) (D+D’)=ABCD+ABCD’+A’BCD+A’BCD’

Resultado final para R= ABD+BC

3. Se suman los TODOS minitérminos.

R= ABD+BCR= ABD+BC = ABCD+ABC’D+ ABCD+ABCD’+A’BCD+A’BCD’

4. Quitando minitérminos repetidos.

R=ABCD+ABC’D+ABCD’+A’BCD+A’BCD’

5. Ordenando queda el resultado final.

R=A’BCD’+ A’BCD+ ABC’D+ ABCD’+ ABCD

6. En forma canónica.

R=(6,7,13,14,15)

Actividad complementaria 3:

---

Dibujar la tabla de verdad para R= ABD+BC y partir de ella construir la forma estándar de R