Reconoce las características básicas de los circuitos secuenciales, a través del estudio de Latch, Flip-Flop, multivibradores, de lógica programable PLD, GALs y memorias ROM y RAM, para construir sus propias definiciones de conceptos, empleados en el diseño de circuitos lógicos programables.

El concepto de circuito secuencial se aplica a aquellos circuitos lógicos en los que sus valores en el estado presente dependen del estado anterior y a su vez condicionan los del estado siguiente. Lo que se ilustra en la figura 69

Figura 48. Estados para un circuito secuencial

Lo explicaremos con un ejemplo sencillo; Se tiene un circuito formado por una batería de 1.5 V, un interruptor y un foco, que forman un circuito secuencial, puesto que para estar encendido el foco , estado presente, debió estar apagado ,estado anterior, y en el ,estado siguiente, el foco estará apagado. Para el estado presente, foco apagado, el estado anterior fue foco prendido y el estado siguiente será foco prendido. En este ejemplo el interruptor es el elemento que proporciona el estado, interruptor cerrado foco prendido y interruptor abierto foco apagado. A esto se le llama elemento de almacenamiento.

Es decir en los circuitos secuenciales la función de salida depende del estado actual más entradas externas, y siempre presenta tres estados: anterior, presente y siguiente. Cabe mencionar que el circuito siempre está en estado presente, ¿ podrías explicar por el qué?.

4.1.1. Latches, flip flops y multivibradores

En los circuitos secuenciales el elemento de almacenamiento que proporciona los estados son los circuitos llamados Flip-Flop en su forma más elemental es un circuito retroalimentado formado por dos compuertas iguales ya sean "And" u "Nor" ver figura 49 a) y b)

Los circuitos llamados Latch o Latches son circuitos Flip-Flop que mantienen el estado de salida Alto o Bajo hasta que son activados para un cambio de estado, en un cambio en el nivel de la señal de entrada, no requieren de una señal temporizadora de sincronía o disparo, son flip-flop elementales y útiles para diseñar circuitos asíncronos. Es decir, no dependen de una señal temporizadora de sincronía. Los circuitos de la figura 49 son latches

En los circuitos se observa que para su funcionamiento se tienen dos entradas S ( set) y R ( reset ) y dos salidas Q y Q' en donde una salida es el complemento de la otra.

Para Q =1 , Q' = 0 se dice que es la condición SET (establecer) y para Q =0 , Q' = 1 se dice que es la condición RESET (restablecer).

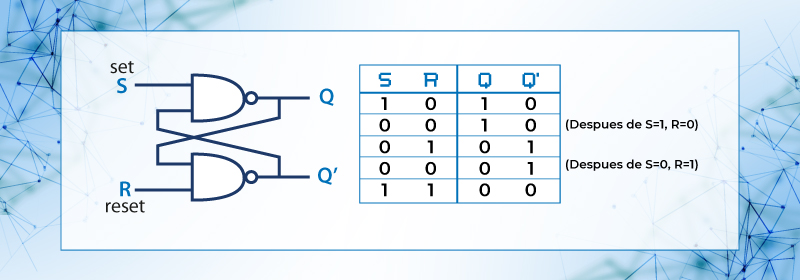
Figura 49 a). latch SR – NAND y Tabla de verdad.

Este es un circuito con dos compuertas NAND con retroalimentación, es decir la salida del primero se conecta a la entrada del segundo y la salida del segundo se conecta a la entrada del primero.

Operación: Normalmente opera con ambas entradas en 1, es decir R = 1 y S = 1, ya sea para que en la salida esté en el valor asignado o para cuando se desea efectuar cambio.

Dejando R = 1 y poniendo la entrada S = 0 se pondrá la salida en Q = 1 , (SET), cuando regresen ambas entradas a 1, y permanecerá en este estado, hasta que se desee hacer cambio, por otro lado dejando S = 1 y poniendo en la entrada R = 0 se pondrá la salida en Q = 0 (RESET) cuando ambas entradas regresen a 1, y permanecerá en este estado, hasta que se desee hacer cambio. Pero si se hace tanto a R = 0 como a S = 0 se produce un estado no definido, por lo que se debe evitar esta condición.

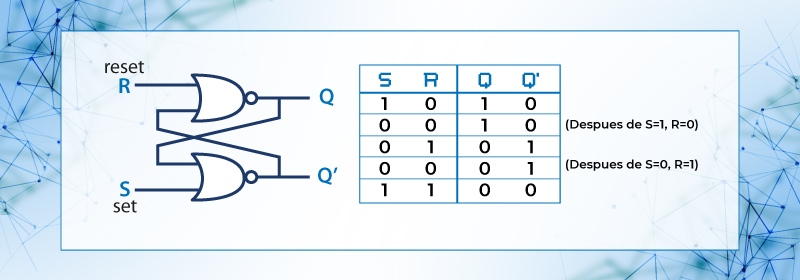
Figura 49 b). latch SR – NAND y Tabla de verdad.

Es un circuito con dos compuertas NOR con retroalimentación, es decir la salida del primero se conecta a la entrada del segundo y la salida del segundo se conecta a la entrada del primero.

Operación: Normalmente opera con ambas entradas en 0, es decir R = 0 y S = 0, ya sea para que en la salida este en el valor asignado o para cuando se desea efectuar cambio.

Dejando R = 0 y poniendo la entrada S = 1 se pondrá la salida en Q = 1 , (SET), cuando regresen ambas entradas a 0, y permanecerá en este estado, hasta que se desee hacer cambio, por otro lado dejando S = 0 y poniendo en la entrada R = 1 se pondrá la salida en Q = 0 (RESET) cuando ambas entradas regresen a 0, y permanecerá en este estado, hasta que se desee hacer cambio. Pero si se hace tanto a R = 1 como a S = 1 se produce un estado no definido, por lo que se debe evitar esta condición.

Latch con señal de control.

Latch con señal de control que permita que un cambio en la entrada afecte al valor establecido.

Esto se logra con el circuito de la figura 50 el cual tiene dos compuertas NAND controladas por una señal C de tal forma que si C = 0 la señal de salida Q no cambia pero si

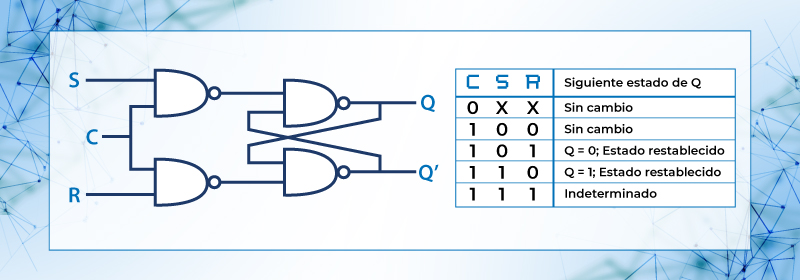
Figura 50. Tabla de verdad del latch SR con señal C de control

Latch D

Este latch se puede construir tanto con NAND como con NOR, y está diseñado para impedir que ambas entradas tengan el mismo valor, pues como ya se dijo se produciría una salida Q = no definida. Es útil para almacenar datos binarios

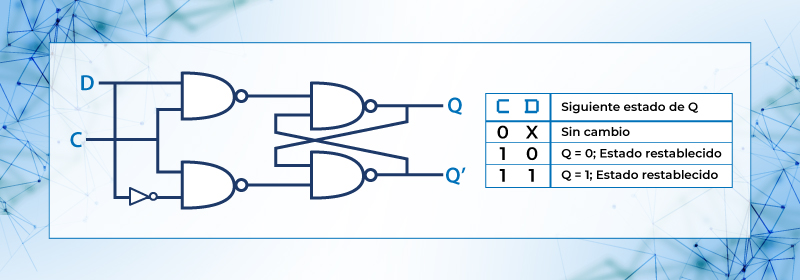
Figura 51. Latch tipo D

Circuitos FLIP-PLOP´s

A un circuito latch se le llama FLIP-PLOP si se construye de tal manera que cambie de estado enviando pulsos de control, cuando se dispare únicamente con una señal de control llamada RELOJ o “CLOCK” al cambiar esta de 0 a 1 o viceversa, entendiendo que solo hace el disparo en el instante del cambio. Al contrario de los circuitos latch que como ya se dijo, el cambio se puede realizar mientras se mantenga el valor de 1.

El que un circuito latch pueda cambiar de estado mientras se mantiene el nivel de disparo provoca que el sistema pueda cambiar de estado varias veces y generar errores, al contrario de cuando solamente se cambia de estado cuando durante el disparo, es decir en el tiempo de transición de la señal

Existen varios tipos de Flip-Flop o F-F todos ellos responden a diferentes señales de excitación, son construidos generalmente en compuertas F-F más circuitos combinacionales, para diferentes tipos de aplicación, aunque es conveniente señalar que para la misma aplicación se puede implementar con cualquier tipo de F-F, obviamente unos presentan mejores ventajas que otros

La mayoría de los circuitos secuenciales se implementan con circuitos tipo JK o tipo D

Flip-Flop tipo D

Este circuito es disparado durante el periodo de transición de 1 a 0 de la señal de reloj esto se logra con dos latch tal como se muestra en la figura 52

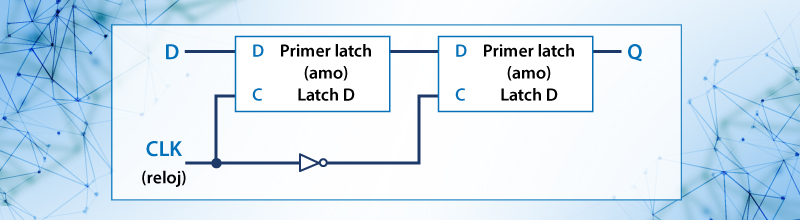
Figura 52. Flip-flop primero-segundo (amo-esclavo)

Para cuando la señal de reloj es 0 la salida del inversor es 1, quedando el segundo F-F habilitado con la señal Q del primer F-F, quedando este primer F-F deshabilitado pues su entrada de reloj es 0

La tabla de excitación son los valores que toma la entrada para que el F-F cambie, como ya se mencionó.

A este Flip-Flop Tipo D también se le llama tipo espejo puesto que la salida Q sigue a la entrada de excitación D

Tabla 32. Tabla de excitación Flip-flop tipo D

Flip-Flop Tipo JK

En la figura 53… se muestra el circuito del F-F tipo JK

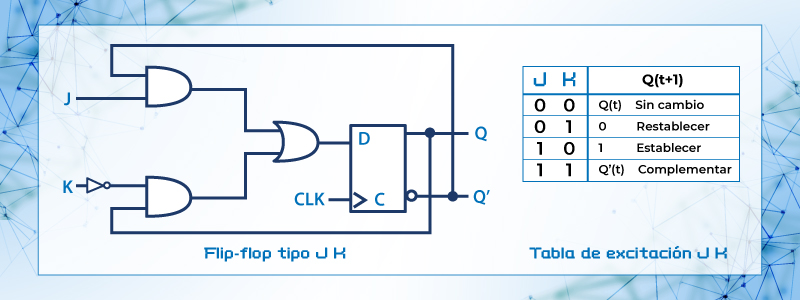
Figura 53. Diagrama de Flip-flop tipo JK

Flip-Flop Tipo T

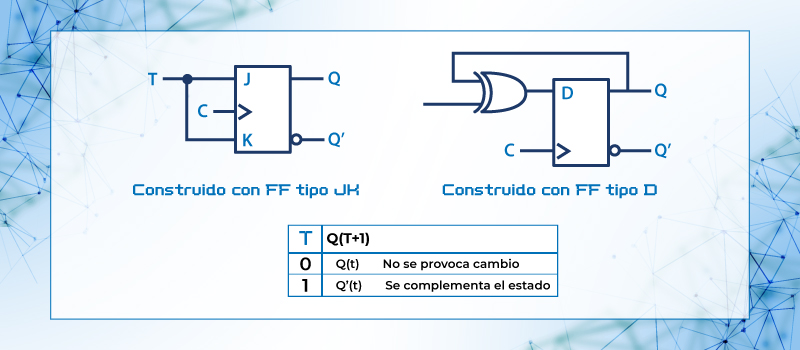
Figura 54. Tabla excitación Flip-Flop Tipo T

Ejemplo 1.-Diseña el circuito para abrir y cerrar una puerta.

SolucionEl latch que se utilizará será tipo D. Suponiendo que se tienen 2 botones, uno para abrir (rojo) y otro para cerrar (verde) la puerta, el diagrama será el siguiente. Se usa un solo botón que mecánicamente está en rojo o verde pero no en ambos.

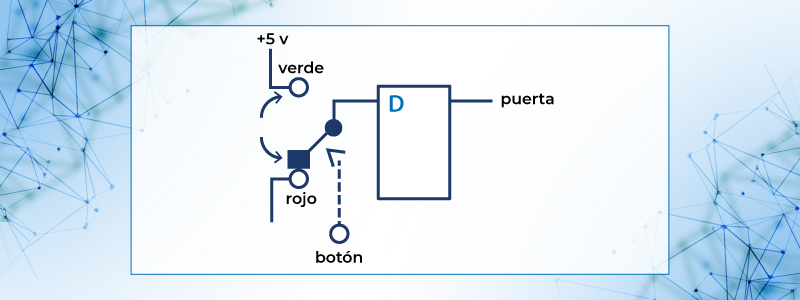
Figura 55. Circuito para abrir y cerrar una puerta.

El funcionamiento de este sistema, es el siguiente:

Cuando se presione el botón ira a rojo, la puerta permanecerá cerrada.

Si se presiona nuevamente estando en rojo, el botón ira a verde, la puerta permanecerá abierta.

No se pueden estar en los dos estados pues mecánicamente lo impide el botón.

Multivibradores

A los circuitos multivibradores también se les conoce como circuitos astable o monoestable.

Circuito astable, el circuito oscila indefinidamente sin necesidad de señal de inicio o disparo.

Circuito monoestable, el circuito cambia a estado alto a partir de una señal de control o disparo.

Al circuito multivibrador astable se les conoce más comúnmente como Circuito de Reloj. Este circuito oscila por sí mismo sin necesidad de señal externa.

Aunque se pueden construir varios tipos de multivibradores u osciladores, el más común es el construido a base del circuito integrado LM555 o comúnmente llamado temporizador 555.

Este tiene la ventaja de que se puede emplear como circuito estable o monoestable.

Es muy usado para generar la señal de reloj que se emplea en los circuitos de FF.

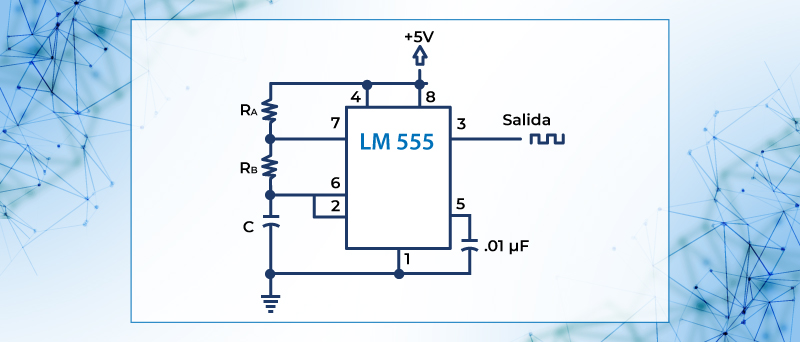
Figura 56. Circuito de reloj empleando CI LM555.

Se muestra el circuito de reloj, el capacitor C se carga a través de RA y RB con los valores de resistencias y el capacitor, se determina el tiempo para la forma de onda.

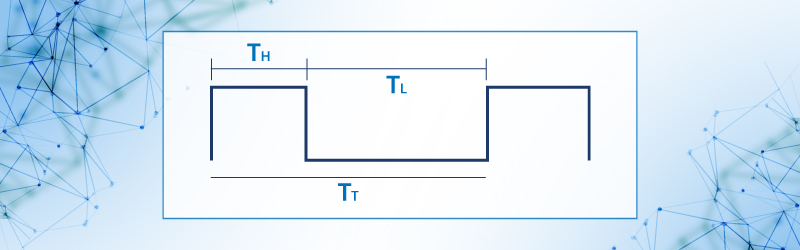
Figura 57. Forma de onda del generador con LM555

La salida a valor alto se determina por el tiempo TH

       TH = 0.693(RA + RB)C ∙∙∙∙∙∙∙∙∙∙ 1

La salida a valor bajo se determina por el tiempo TL

       TL = 0.639 RBC ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2

Luego entonces el tiempo total estará dado por TT= TH + TL

       TT= 0.693(RA +2RB)C∙∙∙∙∙∙∙∙∙∙∙∙∙3

Ejemplo 2.-Determina los valores de C, RA y RB para una señal de reloj de 1 seg. con estado alto y bajo iguales.

Solucion:TH = 0.5 = 0.693(RA + RB)C∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1

TL = 0.5 = 0.639 RBC∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2

En la ecuación 2 hacemos C=1 µF por lo que

TL = 0.5 = 0.639 RB (1x10-6)

RB= 0.5 ∕ 0.693(1x10-6)

RB= 0.7215x10-6 = 721.5 Khom

Para TH=0.5=0.693(RA + RB)C

Fijamos C=1 µF y obtuvimos para RB= 0.7215x10-6 = 721.5 Khom

Por tanto           TH=0.5=0.693(RA + 7215x10-6)( 1x10-6)

RA = 0.5 ∕ 0.693(1x10-6) - 1

RA = 0.7215x10-6 + 1

Despreciando el valor de -1, tenemos que RB = RA = 0.7215x10-6 = 721.5 Khom

Por lo que el circuito queda como

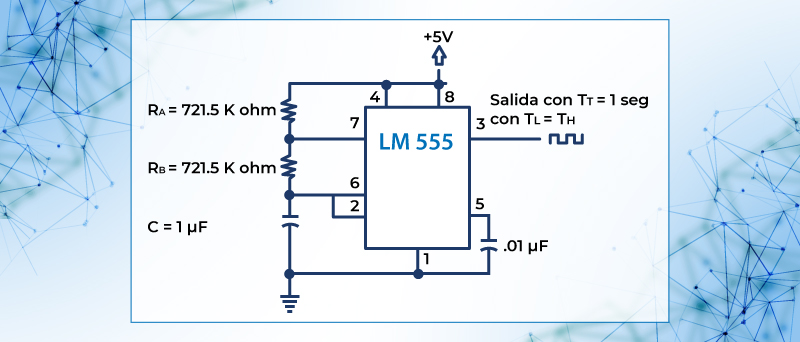
Figura 58. Circuito temporizador para 1 seg con TL= TH

Ejemplo 3.-Diseñar un circuito monoestable con el 555

Circuito monoestable tiene un estado o siempre está en cero o L, pero cuando se pulsa el botón inicia un estado alto H, es decir cada vez que se pulsa el botón inicia un estado alto H, que termina según se haya diseñado el lapso de tiempo.

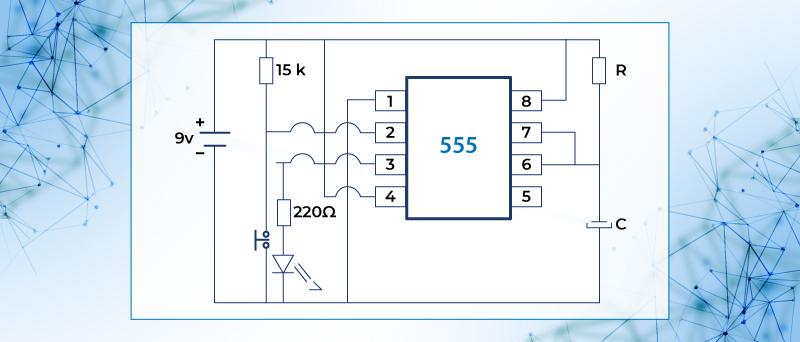
Figura 59. Diagrama del circuito monoestable con el CI 555

Formula del tiempo T= 1.1RC

Para un lapso de tiempo de 1 se quedaría:

Se fija el valor de C= 1 µF entonces T=1=1.1Rx1x10-6

Despejando R se tiene

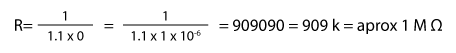
Formula 1. Formula

El circuito quedaría con C= 1 µF y R= 1 M Ω si no se requiere un 1 seg exacto, de lo contrario si hay que poner los valores de diseño.