


Inicio Unidad I Unidad II Unidad III Unidad IV Unidad V Bibliografía

La simplificación de circuitos lógicos por métodos gráficos se puede realizar con diagramas de Venn pero como ya se dijo en el apartado no resulta práctico su uso en representaciones complejas por lo que no es muy común su empleo. La otra solución gráfica es por mapas de karnaugh la cual resulta de fácil aplicación para expresiones de hasta 4 variables, para 5 variables o más es conveniente usar métodos computacionales como por ejemplo la implementación del algoritmo de Quine – McCluskey, los interesados pueden ver el libro de John F. Wakerly, Diseño Digital, · Prentice Hall, 3ra Edición, pág.236. En este libro el autor presenta un programa en lenguaje C para este algoritmo. .
Diagramas o mapas de Karnaugh- Simplificación
Un mapa de Karnaugh es una representación de los miniterminos que proporciona un método sistemático de simplificación, que genera las expresiones suma de productos y productos de suma más simples posibles.
El mapa es similar a una tabla de verdad ya que muestra todos los posibles valores de las variables de entrada y la salida que resulta para cada valor. Su aplicación se ilustra fácilmente con los siguientes ejemplos, se muestra su empleo para 2, 3, y 4 variables.
Mapa de Karnaugh para dos variables.
El mapa de dos variables es un conjunto de 4 celdas, con todas las combinaciones posibles de la siguiente forma:
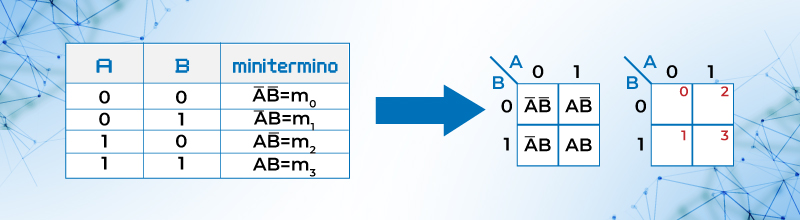
Figura 14. Mapa de Karnaugh para dos variables
Mapa de Karnaugh para tres variables.
El mapa de tres variables es un conjunto de 8 celdas, con todas las combinaciones posibles de la siguiente forma:
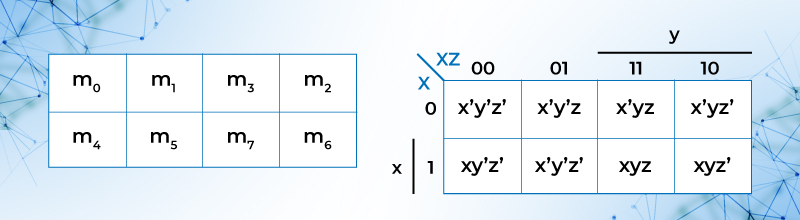
Figura 15. Mapa de Karnaugh para tres variables
Mapa de Karnaugh para cuatro variables.
El mapa de cuatro variables es un conjunto de 16 celdas, con todas las combinaciones posibles de la siguiente forma:
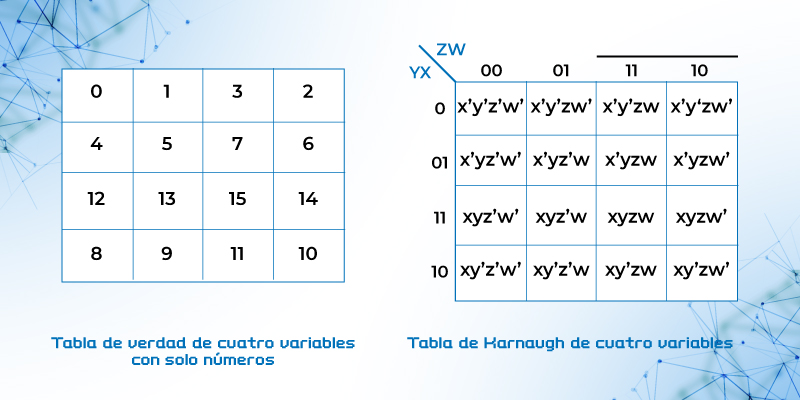
Figura 16. Mapa de Karnaugh para cuatro variables
Uno de los mapas de la figura 17 está mal ¿Cuál es el error?
Ejemplo 24.- Reducir las expresiones a) f = xy y b) Q = xy’ +x’y +
Solución
a) se representa en el mapa como un 1 en la posición indicada, no tiene reducción puesto que es un solo término.
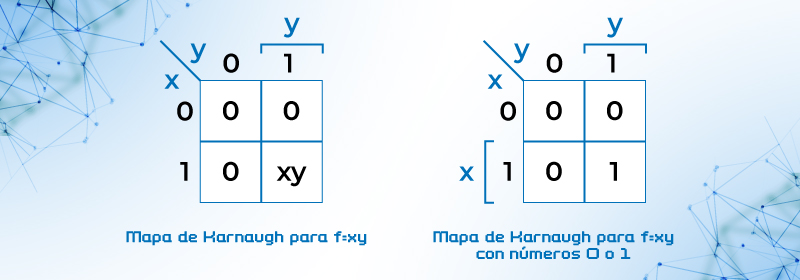
Figura 17. Mapa de Karnaugh para ejemplo a) f = xy
Solución
Para b) Se representan los 1 en la casilla correspondiente, se pueden hacer grupos de 2. Se observa que el par de 1 horizontal ocupa el dominio de x y que el par de 1 vertical ocupa el dominio de y por lo que la expresión queda: Q = x + y.
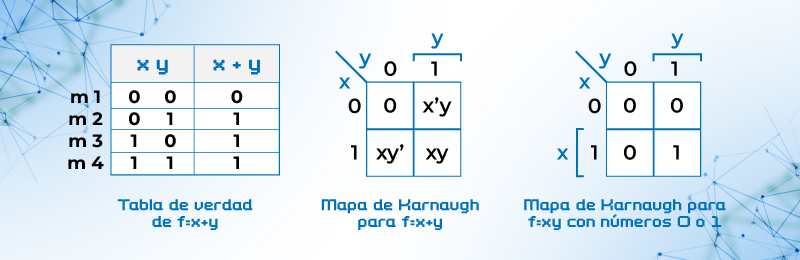
Figura 18. Mapa de Karnaugh para ejemplo b) Q = xy’ +x’y + xy
Ejemplo 25.- a) Simplificar la expresión F(x,y,z) = ∑(0,2,4,5,6)
Solución: Se anotan los 1 en la casilla correspondiente al minitermino indicado, se agrupan los 1 en múltiplo exponencial de 2, esto es 2, 4, 8, 16,.. 2n para este ejemplo como se indica en el diagrama. Se observa el dominio que ocupa y se hace la anotación. Se agrupan los cuatro miniterminos verticales y se observa que ocupa el dominio de Z’, y dos miniterminos horizontales están en el dominio de XY’ por lo que la expresión reducida queda: F = z’ +xy’
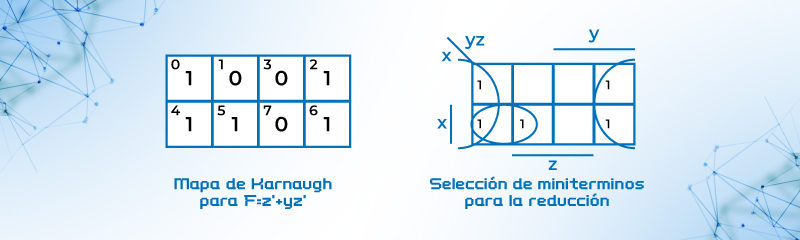
Figura 19. Reducción expresión F(x,y,z) = ∑(0,2,4,5,6)
a) Simplificar la expresión Q = x’yz +xyz +xyz’ + xy’z’
Solución: En el mapa de 3 variables se anotan los 1 en la casilla correspondiente y se agrupan términos adyacentes en múltiplos exponenciales de 2, ver figura, se observa que dominios ocupan. Quedando la reducción como Q = yz + xz’
Es conveniente unir la cadena a fin de evitar errores, esto se hace con el termino XY por lo que la función queda como Q = yz+xz’+xy
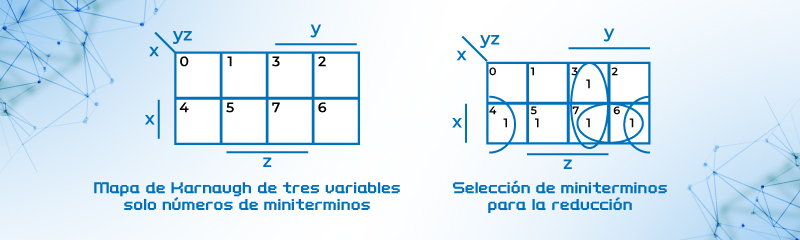
Figura 20. Reducción por mapas de Karnaugh para la expresión Q = x’yz +xyz +xyz’ + xy’z’
Ejemplo 26.- a) Simplificar la expresión Booleana F(w, x,y,z) = ∑(0,1,2,4,5,6,8,9,12,13,14))
Solución: En un mapa de 4 variables se anotan los 1 en la casilla del minitermino correspondiente, se agrupan los términos adyacentes en múltiplos exponenciales de 2 , entre más términos mayor es la reducción, pero estos deben estar en múltiplos exponenciales de 2, ver figura del ejemplo, se han formado tres grupos, uno de 4 términos en la parte superior, otro también de 4 términos en la parte media y un tercero de 8 términos en la parte izquierda. Observando los dominios que ocupan se tiene: F = y’ +w’z’ +xz’.
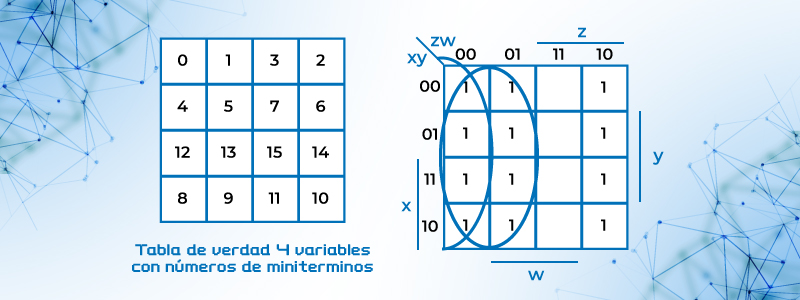
Figura 21. Simplificación de la expresión Booleana F(w, x,y,z) = ∑(0,1,2,4,5,6,8,9,12,13,14))
Ejemplo 26.- b) Simplificar la expresión Booleana Q = A’B’C’ + B’CD’ + A’BCD’ AB’C’
Solución: Primero se debe de completar los miniterminos, esto es:
Q = A’B’C’(D + D’) +’BCD’(A +A’) +A’BCD’ + AB’C’(D +D’) = A’B’C’D + A’B’C’D’ +’BCD’A +’BCD’A’ +A’BCD’ + AB’C’D + AB’C’D’) = ∑(0,1,2,6,8,9,10)) y se sigue el procedimiento ya descrito en apartadoa). Q = B’D’ +B’C’ +A’CD’.
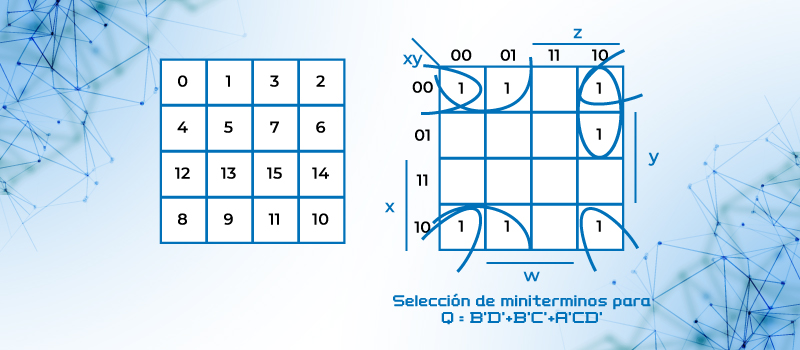
Figura 22. Reducción por mapa de Karnaugh para Q=A’B’C’ + B’CD’ + A’BCD’ AB’C’ = ∑(0,1,2,6,8,9,10), queda como Q = B’D’+B’C’+A’CD’

