Aritmética de funciones

Como ya se dijo resulta de particular importancia el reducir o simplificar las funciones lógicas por el aspecto de costo y operación, pues entre menos compuertas, más económico, pero también entre más sencillo sea un circuito su desempeño resulta más confiable y será más fácil de construir..

Un método de cómo simplificar funciones requiere de aplicar una estrategia para hacerlo, se propone básicamente:.

• Tratar de aplicar los postulados X+X’=1 , X+1=1 , X+X =X pues de esta forma se podrán reducir términos.
• Por observación identificar los términos que contengan variables como X , X’ y que se puedan agrupar por factorización, es decir la propiedad distributiva de la multiplicación respecto a la suma.
• Estar atentos en la aplicación de otros teoremas, como X+XY=X
• Tener mucho cuidado en la aplicación de los teoremas de D’morgan, recordar que los términos se niegan y el operador + (suma) cambia a • (multiplicación) y viceversa.

Esto se explica con los ejemplos siguientes:

Ejemplo 13.- Reducir aplicando álgebra de boole la función Fa y mostrar un diagrama esquemático de las funciones original y simplificada

        Fa = m5+ m6+ m7 = C G’ L + C G L’ + C G L

Se observa que los minitérminos (m5 , m7 ) y (m6 , m7) se pueden factorizar, para sacar provecho de que tienen términos con variables complementarias, esto es m5 tiene a G y m7 tiene a G’ lo mismo para m6 y m7 que tienen a L y L’ respectivamente.

Falarma =

= (C G’ L + C G L) + (C G L + C G L’)

= C L(G’+G) + CG(L+L’)

= C L(1) + CG(1)

= CL+CG

Actividad complementaria 6:

---

Identifique cuales postulados o teoremas se aplican en cada paso

Ejemplo 14.- Simplifique las funciones booleanas al menor número de literales:

1.- x(x’ + y) + xyz = xx’ + xy + xyz = 0 + xy +xyz = xy + xyz = xy

2.- xy + x’z + yz = xy + x’z + yz(1) = xy + x’z + yz(x + x’) = xy +x’z + yzx +yzx’ =xy + x’z + xyz + x’yz = xy(1+z) + x’z(1+y) = xy + x’z

3.- (x + y)(x +y’) = xx +xy’ +xy + yy’ = x + xy +xy’ + 0 = x

Actividad complementaria 7:

---

Identifique cuales postulados o teoremas se aplican en cada paso

El complemento de una función F es F’ y su valor, se obtiene intercambiando ceros por unos y unos por ceros, pero cuando la función se expresa con términos, el complemento se encuentra algebraicamente aplicando los teoremas de Demorgan que es conveniente leerlos así:

• (x+y)’= x’y’ El complemento de la suma de dos términos es igual a el primer término negado por el segundo término negado.
• (xy)’ = x’ + y’ El complemento de un producto de términos es igual a la suma del primer término negado + el segundo término negado.

Ejemplo 15.- Obtener el complemento de las funciones F = x’yz’ + x’y’z y Q=x(y’z’+yz) aplicando los teoremas de D’morgan tantas veces como sea necesario

F’ = (x’yz’ + x’y’z)’ = (x’yz’)’ (x’y’z)’ = (x+y’+z)( x+y+z’)

Q’ = [x(y’z’+yz) ]’ = x’ + (y’z’+yz)’ = x’ + (y’z’)’(yz)’ = x’ + (y+z)(y’+z’)

Un procedimiento más sencillo para obtener el complemento de una función es aplicar el principio de dualidad que estable que toda expresión algebraica que pueda deducirse de los postulados del álgebra booleana seguirá siendo válida si se intercambian los operadores y los elementos de identidad. Si se quiere obtener el dual de una función simplemente se intercambian los operadores OR y AND y se sustituyen los unos por ceros y los ceros por unos.

Para obtener el complemento de una función se intercambian los operadores OR y AND y se complementa cada literal.

Ejemplo 16.- Aplicando el principio de dualidad obtener el complemento de las funciones:

(a).- F = x’yz’ + x’y’z Solución F’ = (x’yz’ + x’y’z)’ = (x+y’+z)(x+y+z’)

Q = x(y’z’+yz) Solución Q’ = [x(y’z’+yz) ]’ = x’ + (y+z)(y’+z’)

Ejemplo 17.- Aplicar los teoremas de De Morgan a las expresiones:

(a).- [(A+B)’+c’]’ (b).- [ (A’+B) + CD]’ (c).- [(A+B)C’D’+E+F’]’

Solucion.- (a) [(A+B)’+C’]’ = (A+B)’’C’’ = (A+B)C (c).- [(A+B)C’D’+E+F’]’ = [(A+B)C’D’]’(E+F’)’ = [(A+B)’+(C’D’)’](E’F) =(A’B’+C+D)E’F

2.3.2. Sistemas digitales, microprocesadores y microcontroladores

Todas las expresiones booleanas pueden ser convertidas a tablas de verdad utilizando los valores binarios de cada término de la expresión. La tabla de verdad es un formato muy común y conciso para expresar el funcionamiento lógico de un circuito pues es cómodo para ver el valor de las entradas y el valor de salida resultante en función de los minitérminos, a partir de la tabla se puede generar la ecuación que define el comportamiento del circuito, como ya se hizo presente en varios ejemplos anteriores. Su aplicación resulta lenta en su desarrollo, pero es fácil de implementar tanto para analizar un circuito como para su diseño.

Ejemplo 18.- Desarrollar una tabla de verdad para la expresión F = a’b’c +abc’ + abc

Solución. De la expresión algebraica podemos observar que la función F la podemos expresar con miniterminos como F = m001 + m110 + m111 = m1 + m6 + m7 por lo que la tabla de verdad es

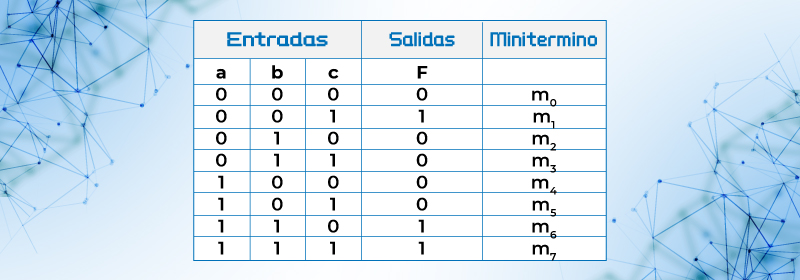
Tabla 14. Tabla de verdad de F = a’b’c +abc’ + abc = m1 + m6 + m7

Ejemplo 19.- Representar en tabla de verdad la función lógica QBA = B’A + B A’

Solución. Expresamos la función Q en minitérminos, esto es QBA= m01+ m10 = m1+ m2

Tabla 15. Tabla de verdad de QBA = B’A + B A’= m1 + m2

Ejemplo 20.- Representar en tabla de verdad la función lógica

QDCBA = B’A + DCB+D’B’A

Solución. Completamos con X las variables faltantes en la función , esto es:

QDCBA = XXB’A + DCBX + D’XB’A

Observar que las literales deben de estar ordenadas en cada término, en este caso el orden es DCBA

En la tabla de verdad valoramos cada término por separado, ponemos 1 para las entradas XX01 que corresponde con XXB’A, 111X →DCBX y finalmente 0X01→ D’XB’A

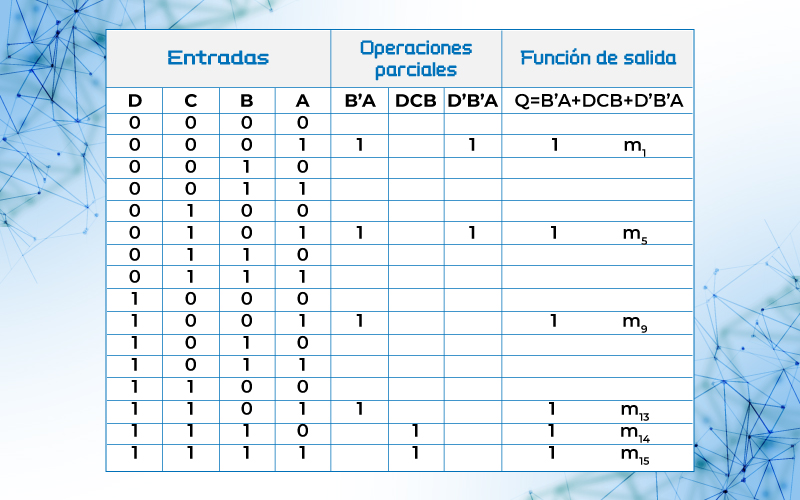
Tabla 16. Tabla de verdad de QDCBA = B’A + DCB+D’B’A = m1+m5+m9+m13+m14+m15

Observación. - Se dejó en blanco las demás casillas para darle claridad a la tabla, pero se debería haber puesto 0 en cada una de estas.

Ejemplo 21.- Desarrollar una tabla de verdad para la expresión F = (AB + AC)’ + A’B’C

Solución. - En la tabla primero valoramos cada termino por separado (operaciones parciales) y al último la función (salida) ya integrada:

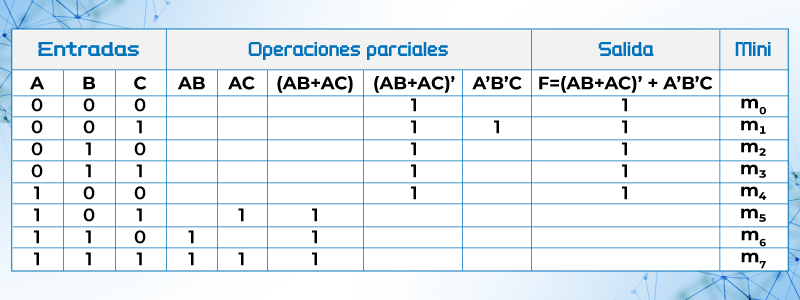
Tabla 17. Tabla de verdad de F = (AB + AC)’ + A’B’C = m0+m1 + m2 + m3+ m4

Ejemplo 22.- Diseñar, usando tabla de verdad, un circuito lógico con tres variables de entrada X; Y; Z que a su salida de, el valor en complemento a 2 de la entrada.

Solución.

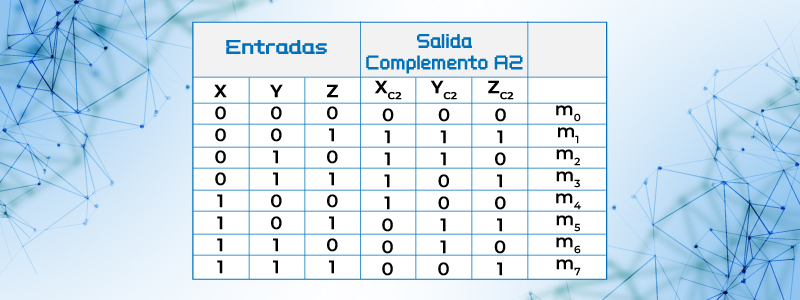
Tabla 18. Tabla que muestra el complemento a dos de las entradas

El circuito tendrá tres salidas de la siguiente forma

XC2 = m1+m2+m3+m4= X’Y’Z+X’YZ’+X’YZ+XY’Z’

YC2 = m1+m2+m5+m6= X’Y’Z+X’YZ’+XY’Z+XYZ’

Zc2 = m1+m3+m5+m7= X’Y’Z+X’YZ+XY’Z+XYZ

Ejemplo 23.- Demuestre con tablas de verdad la validez de la siguiente identidad: QXYZ= X’Y’Z+X’YZ+XY’Z+XYZ = Z.

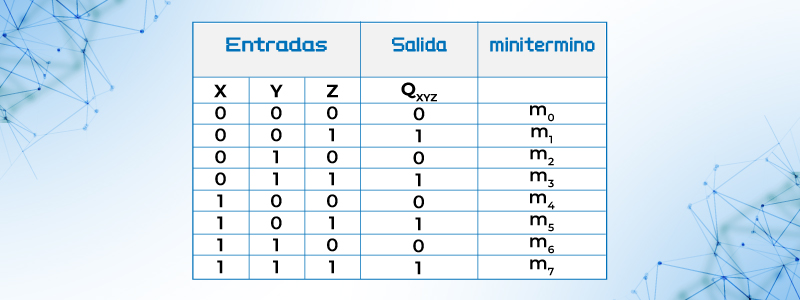
Tabla 19. Tabla de verdad para QXYZ= X’Y’Z+X’YZ+XY’Z+XYZ = Z

En la tabla se puede observar que las columnas para QXYZ y Z son iguales por lo tanto la igualdad es VERDADERA