


Inicio Unidad I Unidad II Unidad III Unidad IV Unidad V Bibliografía

El esquema gráfico de una función Booleana con compuertas.
La principal ventaja de utilizar el álgebra booleana radica en que las operaciones básicas AND, OR y NOT tienen un equivalente directo en términos de circuitos. Estos circuitos reciben el nombre de compuertas lógicas. Las tres compuertas fundamentales reciben el mismo nombre que los operadores, es decir, existen las compuertas AND, compuertas OR y compuertas NOT. La última compuerta recibe el nombre más usual de inversor. Con estas tres compuertas se puede implementar cualquier circuito lógico. .
Ejemplo 8.- Mostrar el esquema de la función Q=AB’ + ABC Solución:
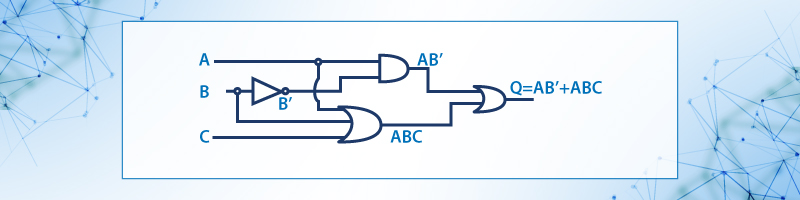
Figura 9. Diagrama esquemático de la función Q=AB’ + ABC
Pero así mismo existen otras compuertas que resultan de la combinación de una compuerta AND con un inversor que se denomina NAND y la compuerta OR con un inversor que se denomina NOR. En la figura 10 mostramos los símbolos tradicionales.
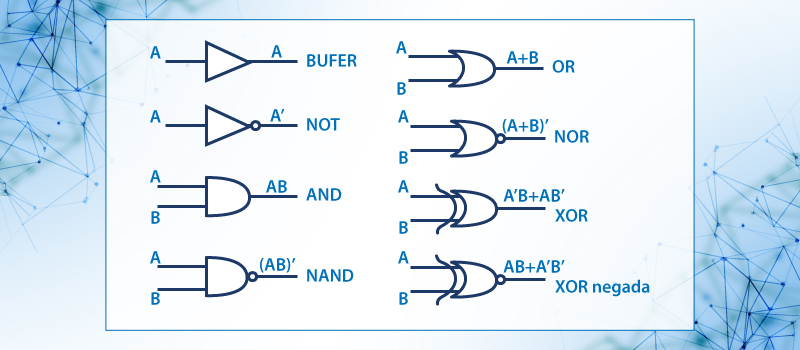
Figura 10. Se muestran los símbolos tradicionales de compuertas booleanas
Es posible demostrar que con únicamente un tipo de compuertas ya sea NAND o NOR se puede implementar cualquier función lógica. Así una compuerta es universal si con solo este tipo de compuerta se puede implementar cualquier función lógica.
Ejemplo 9.- Expresar solamente con compuertas NAND la expresión
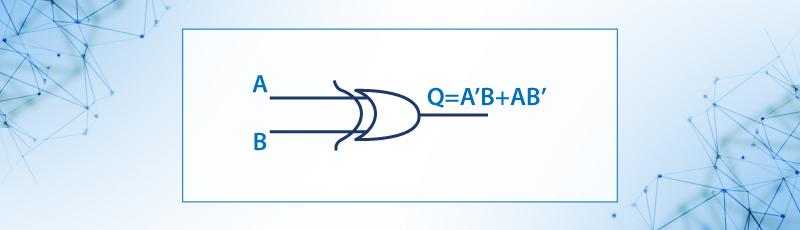
Figura 11. De la función Q = A’B + AB’
Solución .- Conviene negar dos veces la expresión Q, y aplicar los teoremas de Morgan, esto es:
Q = Q’’ = [ (A’B + AB’)’]’ = [ (A’B)’ (AB’)’]’
En donde podemos visualizar las compuertas NAND, (A’B)’ e (AB’)’ para finalmente efectuar el contenido de [ ]’ con otra compuerta.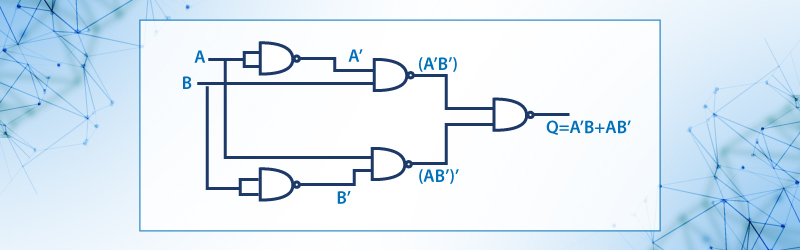
Figura 12. Función Q=A’B+AB’ con solo compuertas NAND
Hacer el diagrama esquemático para Q = A(B+C’) solo con compuertas NAND
Ejemplo 10.- Expresar solamente con compuertas NOR la expresión
Q = A’B + AB’
Solución: Conviene negar dos veces a Q, esto es y aplicar los teoremas de Morgan
Q = Q’’ = [ (A’B + AB’)’]’
En donde podemos visualizar que (A’B + AB’)’ es una compuerta NOR y teniendo presente los teoremas de De Morgan (x +y)’ = x’ + y’ , (xy)’ = x’ +y’, es fácil ver que A’B también se puede representar con una compuerta NOR lo mismo que AB’
Hacer el diagrama esquemático
Cabe señalar que la función X= A’B + AB’ es la compuerta conocida como OR exclusiva o XOR Esta compuerta no es un operador directo. La importancia radica en su amplio uso en la aritmética binaria, siendo la base de la suma. También es muy usada en los circuitos de detección y corrección de errores, implementando funciones de comparación y paridad. El sumador completo, su símbolo y tabla de combinaciones se muestran en la figura 13
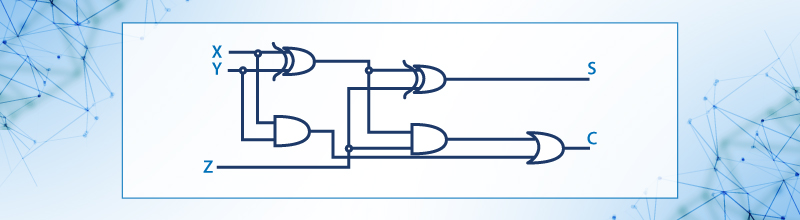
Figura 13. Esquema de verdad para un sumador completo de 3 bit
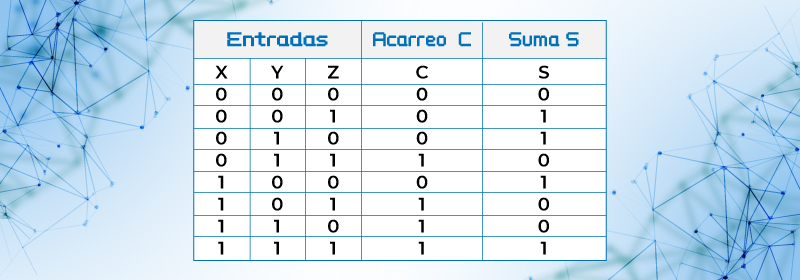
Tabla 13. Tabla de verdad para un sumador completo de 3 bit
Las operaciones binarias NOT, AND, OR NAND, NOR y EXOR y sus posibles combinaciones o arreglos se fabrican con el nombre de compuertas lógicas y de acuerdo con su tecnología se identifican en dos grandes familias, la familia TTL (Transistor Transistor Logic) y la familia CMOS (Complementary MOS) Semiconductores a base de óxido y metal.
La familia TTL se caracteriza porque se maneja un voltaje de alimentación de 5.1 V y corriente promedio del orden de los 10 mmA. Como característica importante es que se pueden manipular manualmente sin ninguna precaución.
La Familia CMOS tiene un voltaje de operación de 3.2 V y consume una corriente promedio de 10 nanoA, ( 10-9 A). Y se debe de tener la precaución para manipularlas de usar ropa de algodón y usar una pulsera conectada a potencial de tierra a fin de evitar descargas eléctricas que pueden destruir la compuerta dada la poca corriente que soportan.
En la unidad V se presenta un estudio de las familias de compuertas con mayor detalle.
Ya se señalaron los diferentes teoremas del Álgebra Boolean en el apartado 2.1.1 su aplicación se verá con mayor detalle en el apartado 2.3.1 Aritmética de funciones.
Teorema de D’Morgan para la negación de la suma { A + B}’ = A’B’ Que se lee: la negación de la suma binaria es igual a multiplicación de entre cada término negado .
Ejemplo 11.- Determinar el valor de la siguiente función después de aplicar el teorema de D’Morgan para la suma:
a.-{ AB’ + A’B}’
Solución { AB’ + A’B} = (AB’)’(A’B)’ Aplicación de teorema D’Morgan para l suma
Teorema de D’Morgan para la negación de la Multiplicación { AB}’ = A’ + B’ Que se lee: la negación de la multiplicación binaria es igual a la suma de entre cada término negado.
Nota: Para resumir, al aplicar los teoremas de D’Morgan: a la suma, ésta cambia a multiplicación y al contrario cuando se aplica a la multiplicación, esta cambia a suma y en ambos casos se niega cada término.
Ejemplo 12.- Determinar la mínima expresión para la función del ejemplo 12 anterior
{ AB’ + A’B}’= (AB’)’(A’B)’ = (A’+B)(A + B’) = Aplicación de teorema D’Morgan para la multiplicación = A’A+A’B’+AB+BB’ = 0 + A’B’+AB+0 = A’B’+AB y la negación de multiplicación de funciones

