


Inicio Unidad I Unidad II Unidad III Unidad IV Unidad V Bibliografía

Un código es un conjunto de símbolos que representar números, letras o palabras. Por ejemplo, el conjunto de puntos y rayas que representan letras y que es conocido como código morse.
En la computadora solo se manejan números binarios, por lo que se hace necesario tener códigos que puedan representar, como ya se dijo, números, letras, secuencias, etc. Es decir, todos los elementos que se quieren representar en una computadora deberán ser con códigos de números binarios.
Código binario directo, como ya se ha visto cualquier número decimal se puede representar con 0s y 1s en un número binario equivalente por ejemplo el número 27 en número binario posicional es 11011 o el número 43.75 es el número binario 101011.11
Pero los seres humanos usamos en general los números decimales, esto significa que con frecuencia se convierte de una base binaria a otra decimal, para facilitar esto se han desarrollado códigos como el Código: Decimal Codificado en Binario ó BCD, por sus cifras en inglés (Binary Code Decimal).
Código BCD
En este código se convierte cada dígito decimal en su código binario directo, cabe mencionar que solo son válidos los equivalentes del 0 al 9 pues únicamente son estos los signos de los números decimales.
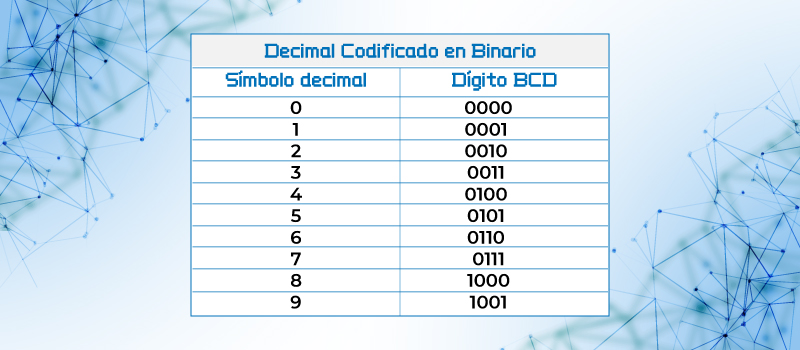
Tabla 4. Números decimales del 0 al 9 en BCD.
Ejemplo convertir los números 45610 y 9762310 a código BCD.
Se codifica cada número decimal en su equivalente BCD en grupo de 4 bits
(456)10 = 4 5 6 = (0100 0101 0110)(BCD)
(97623)10 = 9 7 6 2 3 = (1001 0111 0110 0010 0011)(BCD)
Ejemplo 17a.- Convertir el número BCD = 1110011001100001100 en su equivalente en decimal.
Se divide el número en grupos de 4 dígitos binarios de derecha a izquierda y se convierte cada grupo en decimal, de ser necesario se completa el último grupo de la izquierda con 0s
0111 0011 0011 0000 1100 = 7 3 3 0 6 = 73306
Ejemplo 17b.- Convertir el número BCD = 001110110010 0011 en su equivalente en decimal
0011 1011 0010 0011 = Número prohibido
Se indica error dado que 1011 es número prohibido pues no es código BCD ya que este número binario es mayor que 910
Cabe señalar que a cada uno de los 1s o 0s se le llama bit y que un byte es el conjunto de ocho bits y al de conjunto 4 bit se le llama nibble.
Ejemplo 18.-
a)- 1 0 1 son 3 bits
b) 1011 1010 1110 0001 son 2 Bytes
c) 0001 1100 0011 0000 tiene 12 bits o 2 bytes
c) 00110001 tiene 8 bit o 2 nibbles o 1 byte
Código GRAY
En máquinas que tienen partes giratorias en muchas ocasiones se requiere obtener un codificado numérico de la posición del eje con fines de control, este código es particularmente específico para esta aplicación.
Es un tipo especial de código binario que no es ponderado, es decir los dígitos que componen el código no tienen un peso asignado.
Su característica es que entre una combinación de dígitos y la siguiente, sea ésta anterior o posterior, sólo hay una diferencia de un dígito. Ver tabla 5

Tabla 5. Código GRAY
Este código Gray es utilizado principalmente en sistemas de posición, ya sea angular o lineal.
Sus aplicaciones principales se encuentran en la industria y en robótica. En robótica se utilizan unos discos codificados para dar la información de posición que tiene un eje en particular.
Analizando la tabla anterior se observa que:
La característica de pasar de un código al siguiente cambiando sólo un dígito asegura menos posibilidades de error.

Figura 6. Disco para obtener el código gray en un eje
Explicar cómo se obtiene el código gray a partir del disco mostrado en la figura 6
Buscar en la literatura otros tipos de códigos numéricos y asimismo se sugiere consultar la bibliografía cuando se desee realizar aritmética con números BCD
1.4.2. Códigos alfanuméricos
Las computadoras además de emplear códigos para datos con números deben ser capaces de representar códigos para datos con letras es decir manejar información no numérica. A estos códigos se les llama Alfanuméricos, un código de este tipo debe de incluir todas las letras del alfabeto, mayúsculas y minúsculas, signos deón, caracteres como +,-,$,%,/,>,&, etc. Es decir, todos los signos de un teclado de computadora.
Código ASCII
El código es un estándar realizado en USA Código Estándar Americano para el Intercambio de Información (ASCII) el cual es de 7 bits, por lo que es posible formar 27=128 caracteres diferentes.
Consultar la bibliografía para visualizar y copiar la tabla con código ASCII completa.
Como ya se ha dicho este código se utiliza para manejar información alfanumérica ya sea entre computadoras y dispositivos externos como impresoras, entre otros.
Código para Bit de Paridad
Bit de paridad PAR es un bit que se agrega al grupo de bits que se están transfiriendo y se agrega al grupo para que la suma del bit = 1 sea número PAR, en caso contrario se agrega 0.
Esto es: Sea el número a transferir 1000 0011 entonces con el bit de paridad queda como:
1 1000 0011
Bit 1 de paridad agregado pues la suma de 1s es non.
Ejemplo 19.- Si el número a transferir es 0010 1101 entonces el número con bit de paridad queda como:
0 0010 1101
Bit 0 de paridad agregado pues la suma de 1s es par.
¿Se puede usar Bit de paridad para suma impar o non? Explicar

