


Inicio Unidad I Unidad II Unidad III Unidad IV Unidad V Bibliografía

Los módulos aritméticos son circuitos digitales que realizan las operaciones de suma, resta, multiplicación y división. Que son muy empleados en los sistemas digitales, sobre todo en los programables, como son, calculadoras, microcontroladores y microprocesadores entre otros.
Medio sumador
Para la operación aritmética de suma con dos variables de entrada con un bit, A + B = S, tenemos:
0 + 0 = 1
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 y acarreo 1
En donde podemos observar que, si las dos variables de entrada son uno, se requiere de un bit adicional llamado Acarreo o " Carry"
Diseñando un circuito combinacional para la suma de A + B con un bit de entrada tenemos
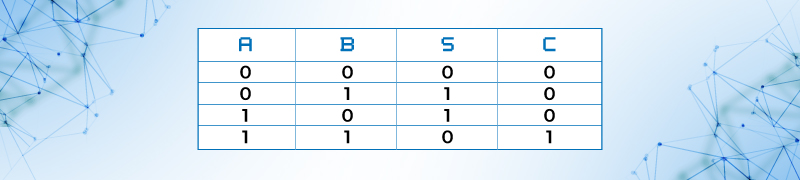
Tabla 27. Tabla de verdad del circuito medio sumador
X + Y = C S
El bit de acarreo es 0 a no ser que ambas entradas sean 1
S = A’·B + A·B
Por consiguiente, la salida S también puede expresarse en términos de la operación OR – Exclusiva:
S= x ⊕ Y
El bit de acarreo C es 1, sólo cuando A y B tienen el valor de 1; por tanto, entre A y B se puede establecer una operación AND:
C= A·B
El diagrama del medio sumador queda como se muestra en la figura 51
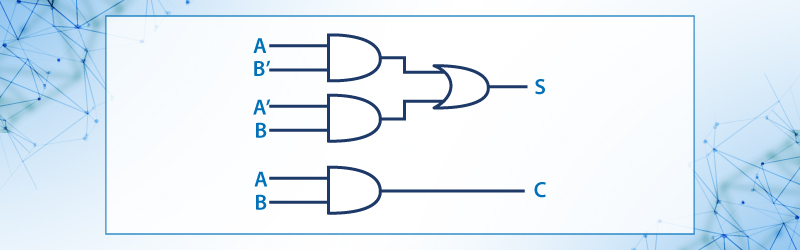
Figura 34: Circuito Medio Sumador..
El circuito del medio sumador con compuertas AND y OR exclusiva queda:
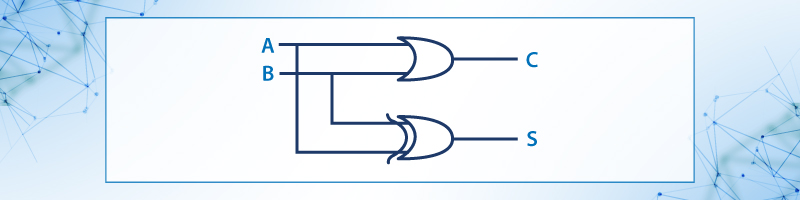
Figura 35: Circuito del medio sumador con compuertas AND y OR exclusiva.
La figura 52 muestra el símbolo lógico del sumador medio. En el circuito las entradas son A y B y la salida S corresponde a la suma y Cout acarreo de salida.
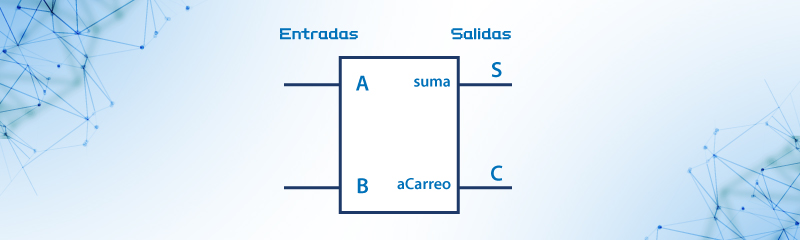
Figura 36: Símbolo lógico del sumador medio.
Sumador Completo
El sumador completo acepta dos bits y un acarreo de entrada y genera una suma de salida junto con el acarreo de salida. La Figura 53 muestra la tabla de verdad del sumador completo. Las entradas A, B y Cen denotan al primer sumando, el segundo sumando y el acarreo de entrada. Las salidas S y Cac representan a la suma y el acarreo de salida.
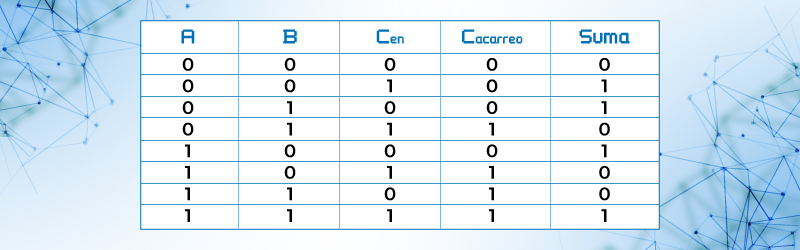
Tabla 28. Tabla de verdad del sumador completo
La salida S en la tabla de verdad corresponde a la operación OR- Exclusiva:
S = A·B’·Cen’ + A’·B·Cen’ + A·B·Cen + A’·B’·Cen
S = Cen’·(A·B’ + A’·B) + Cen ·(A·B + A’·B’)
S = Cen’·(A·B’ + A’·B) + Cen ·(A’·A + A’·B’ + A·B + B·B’)
S = Cen’·(A·B’ + A’·B) + Cen ·((A’ + B)·(A + B’))
S = Cen’·(A·B’ + A’·B) + Cen ·((A·B’)’·(A’·B)’)
S = Cen’·(A·B’ + A’·B) + Cen ·(A·B’ + A’·B)’
El mapa de karnaugh de la salida Cacarreo = C0 como se muestra en la Figura 55 La salida Co está dada por:
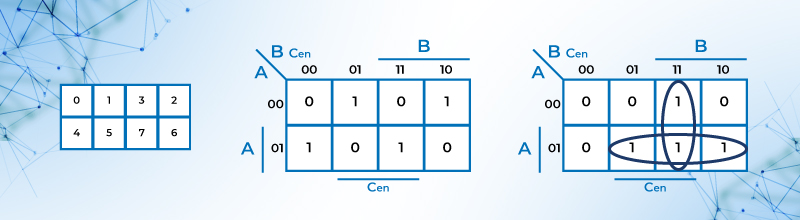
Figura 37: Mapa de Karnaugh salida Suma S y acarreo C0 del sumador completo.
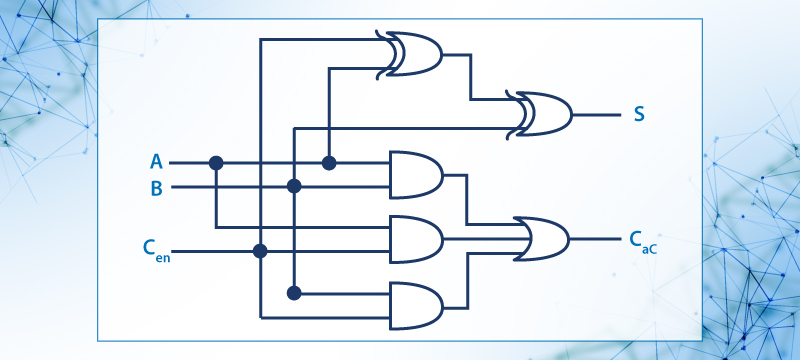
Figura 38: Circuito Lógico del Sumador Completo.
El circuito para el sumador completo también se puede realizar con dos medio sumadores
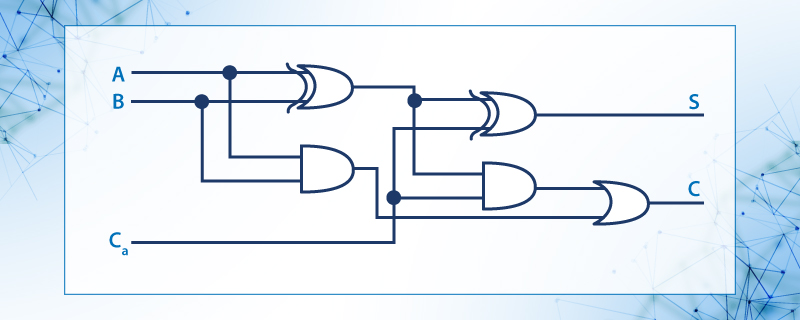
Figura 39: Circuito sumador completo realizado con dos medio sumadores.
demostrar que
S= Cos⊕ (A ⊕ B)
son equivalentes a
S = A´B' Cen + A' B C'en + A B' C'en + A B Cen
Cs = A B + A Cen + B Cen
En esta unidad únicamente se quiere mencionar que con sumadores completos se puede formar una unidad aritmética lógica. No es propósito en esta unidad mostrar cómo se diseñan, para esto se sugiere consultar la bibliografía.
Para realizar las operaciones aritméticas de suma, resta multiplicación y división, se hace uso de la Unidad aritmética lógica (ALU) por sus cifras en Inglés (Arithmetic Logic Unit), es por así decirlo el corazón de las máquinas aritméticas Calculadoras y de las Máquinas programables o computadoras, pero curiosamente la operación aritmética que realiza es la suma, pero eso sí a una velocidad tremenda, actualmente entre 150 a 200 millones de operaciones por segundo.
Esto es así, porque como ya se ha visto anteriormente, la resta se puede efectuar usando complemento a dos y realizando sumas, la operación de multiplicar por una serie de sumas y la división por una serie de restas. Para las operaciones lógicas Negación, And y Or se usa lógica combinacional.
Funcionamiento de la Unidad Aritmética y Lógica (ALU)
Una unidad aritmética lógica puede realizar un conjunto de operaciones aritméticas básicas y un conjunto de operaciones lógicas, a través de líneas de selección. En inglés ALU significa Arithmetic Logic Unit (Unidad Aritmética Lógica). La figura 58 muestra el diagrama de bloques de una ALU.
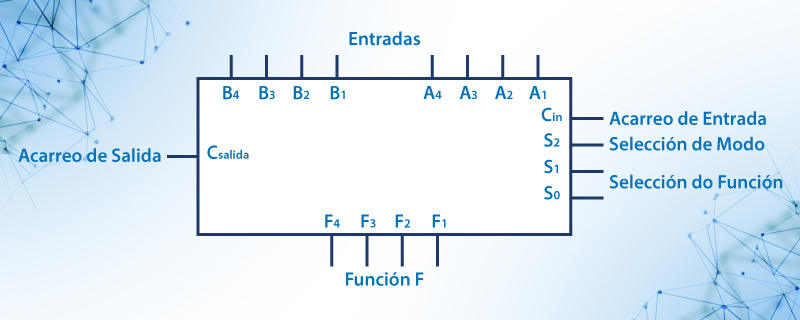
Figura 40: Diagrama de bloques de una ALU.
Las cuatro entradas de A se combinan con las de B generando una operación de salida de cuatro bits en F. La entrada de selección de modo S2 distingue entre las operaciones aritméticas y lógicas. Las entradas de selección S0 y S1 determinan la operación aritmética o lógica. Con las entradas S0 y S1 se pueden elegir cuatro operaciones aritméticas (con S2 en un estado) y cuatro lógicas (con S2 en otro estado). Los acarreos de entrada y salida tienen sentido únicamente en las operaciones aritméticas. El diseño de una ALU implica el diseño de la sección aritmética, la sección lógica y la modificación de la sección aritmética para realizar las operaciones aritméticas y lógicas.
Sección Lógica
Los datos de entrada en una operación lógica son manipulados en forma separada y los bits son tratados como variables binarias. En la figura 59 se listan cuatro operaciones lógicas OR, OR - Exclusiva, AND y NOT. En el circuito, las dos líneas de selección (S1, S0) permiten seleccionar una de las compuertas de entrada, correspondientes a la función Fi.
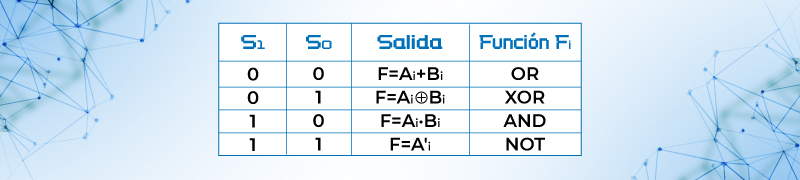
Tabla 29. Tabla de Función Lógica.
El circuito lógico es una etapa de un circuito lógico de n bits.
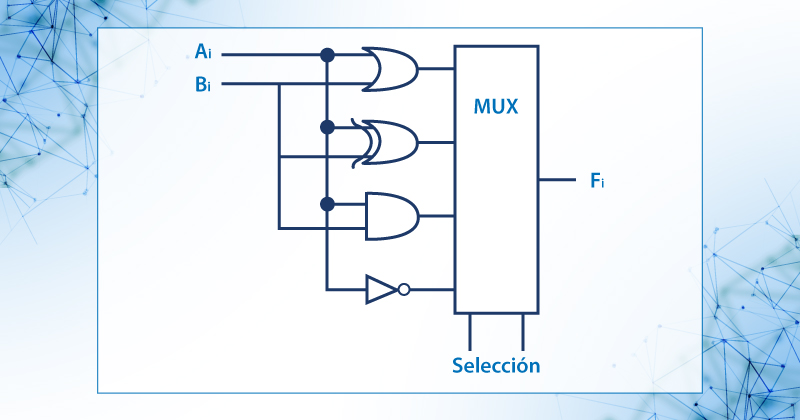
Figura 63: Diagrama lógico de un circuito lógico de una ALU.
Sección Aritmética
El componente básico de la sección aritmética es un sumador en paralelo. Las operaciones aritméticas configuradas en el circuito aritmético se presentan en la tabla 3.12. En una ALU, la suma aritmética se puede implementar con un número binario en A, otro número en la entrada B y el acarreo de entrada Cin en un valor lógico 0. El resto de las funciones se enuncian en la columna descripción.
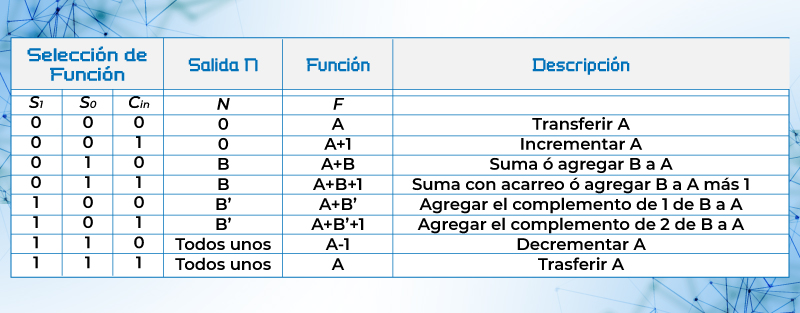
Tabla 30. Tabla de las funciones de un Circuito Aritmético.
No es propósito de esta unidad la implementación de las funciones
Cabe mencionar que existen CI que realizan esta función y se pueden emplear en diseños sencillos propios. Entre otros tenemos: ALUs TTL de 4 bits, como las 74382 y 74481 entre otras.

