


Inicio Unidad I Unidad II Unidad III Unidad IV Unidad V Bibliografía

Una característica de los sistemas digitales es su capacidad para manipular elementos discretos de información. Todo conjunto restringido a un número finito de elementos contiene información discreta. Ejemplos de conjuntos discretos son los 10 dígitos decimales, las 28 letras del alfabeto, y las 64 casillas de un tablero de ajedrez.
En casi todos los sistemas digitales actuales, las señales que se manejan emplean sólo dos valores discretos, por los que se les llama Binarios. Un dígito binario, se le llama Bit y este solo tiene dos valores: 0 y 1.
Existe una correspondencia entre los números binarios que son por así decir, los que “entienden” los sistemas digitales y los números decimales que entendemos los seres humanos.
Los números decimales se expresan en lo que se conoce como Sistema numérico posicional, porque los dígitos del 0 al 9 adquieren valor diferente de acuerdo a la posición que ocupan en un número decimal, por ejemplo el número N = 5278.36 representa una cantidad igual a 5 millares más 2 centenas más 7 decenas más 8 unidades con 3 décimas y 6 centésimas. Este número también se puede expresar como:
N = 5278.36 = 5 x 103 + 2 x 102 + 7 x 101 +8 x 100 . 3 x10-1 + 6 x 10-2
Notación en la que se observa lo siguiente: Por convención el número N se representa normalmente por los coeficientes y se deducen las potencias de 10 por la posición que ocupa cada coeficiente.
La potencia se enumera a partir del punto decimal de derecha a izquierda empezando con el número 0 para los números enteros, y para los decimales de izquierda a derecha a partir del punto decimal empezando con el número -1.
Se dice que el sistema decimal es base 10 porque usa 10 dígitos, del 0 al 9, y los coeficientes se multiplican por potencias de 10.
Al sistema que tenga dos dígitos, 0 y 1, y sus coeficientes se multipliquen por potencias de 2 se le llama sistema de base 2 o números binarios. Al sistema de 8 dígitos, de 0 al 7, y sus coeficientes se multipliquen por potencias de 8 se le llama sistema de base 8 o números octales y así sucesivamente. En la tabla 1 se muestran las equivalencias entre sistemas numéricos de diferente base.
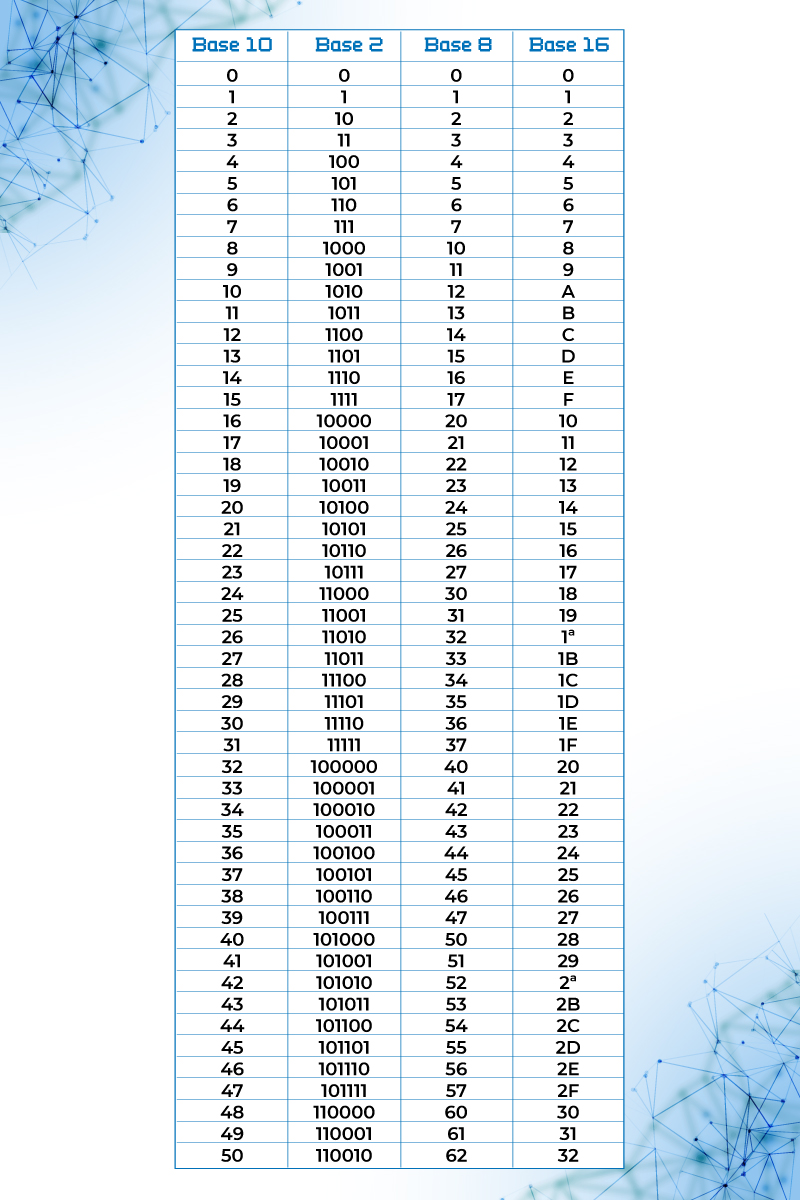
Tabla 1. Sistemas de numeración en diferente base
1.3.1. Conversión entre sistemas
Para distinguir entre números con diferente base, se encierran los coeficientes en paréntesis y se añade un subíndice que indica la base empleada.
La conversión entre sistemas de base n a base 10 se efectúa como se muestra en los ejemplos siguientes:
Ejemplo 3.- Convertir (2403)7 → ( )10
(2403)7 = 2x73 + 4x72 + 0x71 + 3x70 = 2x343 + 4x49 + 0x7 + 3x1 = (885)10
Ejemplo 4.- Convertir (01 0011)2→ ( )10
(01 0011)2 = 1x24 + 0x23 + 0x22 +1x21 + 1x20 = 1x16 + 1x2 + 1x1 = (19)10
Ejemplo 5.- Convertir el número con decimales (63.125)8 → ( )10
Primero se convierte la parte entera
(63)8 = 6x81 + 3x80 = 48 + 3 = (51)10
En seguida la parte decimal
(0.125) = 1x8-1 + 2x8-2 + 5x8-3 = 1/8 + 1/64 + 1/512 = 0.1250 + .0156 + 0.0019 = 0.1425
Finalmente el número se forma con la parte entera y la parte decimal
Por tanto (63.125)8 = (51.1425)10
Ejemplo 6.- Convertir el decimal binario (0100.11)2 → ( )10
1º la parte entera
(1002 =1x22 +0x21 + 0x20 . 1x2-1 + 1x2-2 = 1x4 + 0x 21+ 0x1 = 410
En seguida la parte decimal
(0.11) = 1x2-1 + 1x2-2 = ½ + ¼ = 0.500 + 0.250 = 0.750
Finalmente el número se forma con la parte entera y la parte decimal
Por tanto (0100.11)2 = (4.750)10
La conversión de base 10 a base n, se explica fácilmente con los siguientes ejemplos:
Ejemplo 7.- Convertir el número entero 1910 a número binario
(19)10 → ( )2
Solución
Se divide el entero 19 entre el número de base a la que se quiere convertir, en este ejemplo es entre 2, a fin de obtener entero y residuo, de la siguiente forma:
19/2 = 9 y residuo 1
9/2 = 4 y residuo 1
4/2 = 2 y residuo 0
2/2 = 1 y residuo 0
½ = 0 y residuo 1
se divide hasta que el entero resultante es 0.
El número binario se forma tomando los residuos en orden de abajo hacia arriba por tanto (19)10 → (10011)2
Ejemplo 8.- Convertir el número entero 88510 a número base 7 (885)10 → ( )7
Solución
Se divide el entero 885 entre el número de base a la que se quiere convertir, en este ejemplo es entre 7, a fin de obtener entero y residuo, de la siguiente forma:
885/7 = 126 y residuo 3
126/7 = 18 y residuo 0
18/7 = 2 y residuo 4
2/7 = 0 y residuo 2
El número base 7 se forma tomando los residuos en orden de abajo hacia arriba
por lo tanto (885)10 → (2403)7
Ejemplo 9a.- Convertir el número decimal 0.53410 a número base 2 con 8 Bits
(0.534)10 → ( )2
Solución
Como se trata de un número decimal, se multiplica por el número de base a la que se quiere convertir, en este ejemplo es por 2, a fin de obtener entero y decimal, de la siguiente forma:
0.534 x 2 = 1 . 068 entero 1
0.068 x 2 = 0.136 entero 0
0.136 x 2 = 0.272 entero 0
0.272 x 2 = 0.544 entero 0
0.544 x 2 = 1.088 entero 1
0.088 x 2 = 0.176 entero 0
0.176 x 2 = 0.352 entero 0
0.352 x2 = 0.704 entero 0
0.704 x 2 = 1.408 entero 1
Se termina de multiplicar en dos casos, cuando se obtenga decimal 0.0000 ó cuando se tenga el número de bits deseado. En este ejemplo a 8 bits.
El número base 2 o binario se forma tomando los enteros en orden de arriba hacia abajo
Por tanto (0.534)10 → (0.1000 1000 )2 con 8 bits
Ejemplo 9b.- Convertir ( 13.1250)10 → ( )2 con 8 bits en la parte decimal.
(13)10 → ( )2
Parte entera
13/2 = 6 y residuo 1
6/2 = 3 y residuo 0
3/2 = 1 y residuo 1
½ = 0 y residuo 1
por tanto (13)10 → ( 1101 )2
Parte decimal ( 0.1250)2 → ( )2
0.125 x 2 = 0.250 entero 0
0.250 x 2 = 0.500 entero 0
0.500 x 2 = 1.000 entero 1
0.000 x 2 = 0.000 entero 0
0.000 x 2 = 0.000 entero 0
0.000 x 2 = 0.000 entero 0
0.000 x 2 = 0.000 entero 0
0.000 x 2 = 0.000 entero 0
Por tanto ( 0.1250 )10 → ( 0.0010 0000 )2
Finalmente el número se forma con la parte entera y la parte decimal
(13.1250)10 → ( 1101. 0010 0000 )2 con 8 bits en la parte decimal.
En la práctica son muy usados los números en base 10, base 2, base 8 y base 16
En razón a que 21 = 2, 22 = 4 , 23 = 8 y 24 = 16 y esto facilita la conversión entre las diferentes bases
Ejemplo 10.- Convertir 12410 a ( )2 , a ( )8 y a ( )16
Primero 124 a base 2
124 ÷ 2 = 62 residuo 0
62 ÷ 2 = 31 residuo 0
31 ÷ 2 = 15 residuo 1
15 ÷ 2 = 7 residuo 1
7 ÷ 2 = 3 residuo 1
3 ÷ 2 = 1 residuo 1
1 ÷ 2 = 0 residuo 1
0 ÷ 2 = 0 residuo 0
12410 a ( 0111 1100 )2
Ahora (0111 1100)2 se puede pasar fácilmente a base 8 tomando de 3 en 3 de derecha a izquierda los dígitos de base 2 e indicar el número correspondiente en base 10
Esto es ( 01 111 100 )2 = ( 1 7 4 )8
Y para base 16 se toman de 4 en 4 también de derecha a izquierda los dígitos de base 2 e indicar el número correspondiente en base 10
Teniendo en cuenta que en base 16 los dígitos empleados son 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, y F
Por lo que (0111 1100)2 = ( 7 A)
Observar que teniendo el número en base 2 sólo basta tener en cuenta el número exponencial de 2 para agrupar según sea: de 3 3n 3 para base 8 y de 4 en 4 para base 16
Pasar de base 16 a base 8 y a base 2 el número ( B37)16
Números binarios con representación: signo-magnitud, complemento 1 y complemento a 2
Que es un número en representación a complemento y para qué sirve.
En los sistemas digitales el procesador matemático solo hace sumas, pero eso sí a una gran velocidad, luego entonces cómo se hace la resta u operaciones lógicas de números sumando.
El complemento a un número se establece como el complemento a la base o el complemento a la base disminuida, es decir para números en base diez se tiene el complemento a 10 y el complemento a 9. En números en base 2 o binarios se tiene el complemento a 2 y el complemento a 1.
Para responder a cómo se hace la resta sumando, vemos primero lo siguiente:
Como se hace la resta sumando; veamos:
Realizar la operación 7 - 4 usando complemento a 10
Se deja el valor del minuendo 7
Se pone el complemento a 10 del sustraendo y se suma + 6
Existe acarreo se elimina 13
Se tiene el resultado 3
Para las operaciones aritméticas con números binarios se verá en capítulos siguientes.
Primero nos referimos a cómo obtener el complemento a 1 o a 2 de un número binario.
Complemento a 1 de un número binario:
Para obtener el complemento a 1 de un número binario basta con cambiar los 1 por 0 y los 0 por 1, esto es:
Complemento a 1 del N= 11001100 es 00110011
Esto se escribe Nc1=00110011
Para obtener el número original a partir del complemento a 1, basta con volver a cambiar los 0 por 1 y los 1 por 0, esto es determinar el valor del número X si
Xc1=0101010011 por tanto X = 1010101100
Complemento a 2 de un número binario:
Para obtener el complemento a 2 de un número se obtiene el complemento a 1 y después al número resultante se le suma 1, esto es:
Obtener el complemento a 2 de N=11001100
N= 11001100 es 00110011
Complemento a 1
Complemento a 1 00110011
se le suma 1 + 1
___________
00110100
Por lo que complemento a 2 queda como 00110100
Otra manera más rápida y cómoda de hacerlo es:
Al número a complementar a 2
Se le respeta el primer 1 de derecha a izquierda y se cambian todos los demás 0 por 1 y 1 por 0 esto es
a) Complemento a 2 de N=01001100 = 10110100
b) Complemento a 2 de Q=10001000 = 01111000
c) Complemento a 2 de R=1000111001 = 0111000111
Para obtener el número original a partir del complemento a 2, se hace lo mismo que anteriormente, esto es
a) Obtener el número Q si
Qc2=0101010011 por tanto Q = 1010101101
b) Obtener el número R si
Rc2=1111000 por tanto R =0001000
Para la representación de números binarios se tienen tres formas diferentes de hacerlo: Representación signo magnitud:
Los números positivos se representan con el primer bit a la extrema izquierda con 0 que representa el signo +, seguido por la magnitud.
Para los números binarios negativos un 1 a la extrema izquierda representa el signo - o negativo, seguido de la magnitud, por tanto
0 111 representa el número +7 y 1 111 representa el número -7
Representación complemento a 1
Para obtener el número original en base 10 a partir de la representación en complemento a 2, se debe considerar dos casos:
Los números con signo que se pueden representar dependen de la cantidad de bits que se emplean, en la tabla 2 se muestran los números binarios positivos y negativos que se pueden representar con cuatro bits.
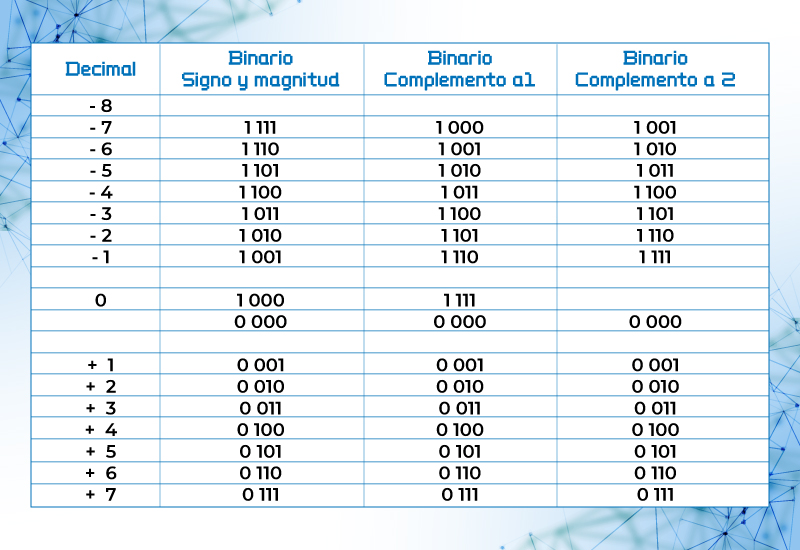
Tabla 2. Representación de números binarios positivos y negativos utilizando 4 bits
Es muy importante notar en la tabla 2 que el número 0 solo tiene una representación en complemento a 2.
Para reforzar el entender la representación de números binarios negativos la explicaremos con los siguientes ejemplos.
Ejemplo 11.- Representar el número (-17)10 en forma binaria con 8 bits, en las formas a) signo y magnitud, b) complemento a 1 c) complemento a 2.
Solución
a) Representación de (-17)10 en forma binaria con signo y magnitud
La convención para representar el bit de signo es 0 para el “+” y 1 para el “ - ” en los tres casos, según se puede observar en la tabla 2. Para la magnitud en este caso basta con representarla con su valor en binario, esto es
(-17)10 → (1 0010001)2
b) Representación de (-17)10 en forma binaria con complemento a 1 con 8 bits
La convención para representar el bit de signo es como ya se dijo: 0 para el “+” y 1 para el “ - ”. Para expresar la parte de magnitud negativa primero es necesario tomar su complemento a 1.
El complemento a 1 de un número se obtiene cambiando todos los “1” del número por “0” y los “0” por “1” Esto es
(17)10 → (0001 0001)2
Entonces el complemento a 1 de 0001 0001 es 1110 1110
Por lo tanto, la representación de (-17)10 en forma binaria con complemento a 1 y con 8 bits, es 1 110 1110
-17C1 = 1 110 1110
c) Representación de (-17)10 en forma binaria con complemento a 2 y con 8 bits
Para expresar la parte de magnitud negativa primero es necesario tomar su complemento a 2.
El complemento a 2 de un número se obtiene tomando el complemento a 1 del número y después sumando 1 al resultado, esto es:
Número a complementar a 2 0001 0001
Complemento a 1 es 1110 1110
Sumar 1 +1
Complemento a 2 1110 1111
O como ya se dijo otra manera más rápida y cómoda de hacerlo es:
Al número a complementar a 2
Se le respeta el primer 1 de derecha a izquierda y se cambian todos los demás 0 por 1 y 1 por 0 esto es
El complemento a 2 de N=0001 0001 es 1110 1111
Entonces la representación de (-17)10 en forma binaria con complemento a 2 y con 8 bits es: NC2= 1110 1111
Ejemplo 12.-
a) El número A = 1110 0011 está en representación en complemento a 1, de que número en base diez se trata.
Solución:
Primero se convierten los 1 por 0 y los 0 por 1
Complemento a 1 de A = 1110 0011
A = - 0001 1100
En base diez → A = - 28
b) El número B = 1011 0001 está en representación en complemento a 2, de qué número en base diez se trata.
A tener en cuenta: Se asigna el peso correspondiente a todos los dígitos 1, tener presente que se considera, que el peso del dígito de signo es negativo, siendo los demás positivos; realizar la suma en base diez:
128 64 32 16 8 4 2 1
1 0 1 1 0 0 0 1
-128 + 32 + 16 + 1 = - 79
→ B = - 79
1.3.2. Operaciones aritméticas básicas
Operaciones de suma y resta con números binarios.
La operación de suma binaria se puede realizar en base a la siguiente tabla:
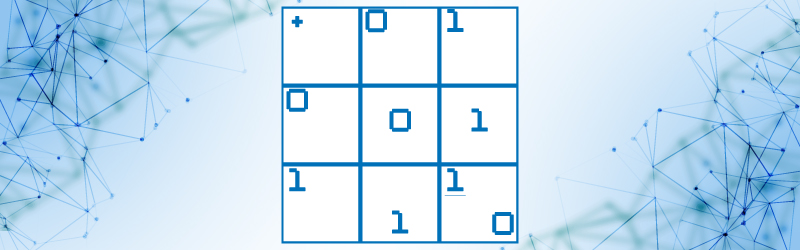
Tabla 3. Tabla de suma con números binarios
En esta tabla el último cuadro se debe leer, 1 +1 resultado 0 y acarreo 1, su aplicación se muestra con los siguientes ejemplos:
Ejemplo 13.- Sea M = 01011 y N = 00110 efectuar M+N
Solución M 10 11 10 1 1
● N + 0 0 1 1 0
Q = 1 0 0 0 1
Ejemplo 14.- Sea A = 1110 0011 y B = 0010 1111 efectuar A+B
Solución A 10 11 1 10 10 10 11 1
● B + 0 0 1 0 1 1 1 1
C = 1 0 0 1 0 0 1 0
1.3.3. Operaciones con complemento
Resta de números binarios
La resta comúnmente se realiza usando el complemento a 1 o el complemento a 2, la forma de hacerlo es similar en ambos métodos, al minuendo se le suma el complemento que corresponda, teniendo cuidado en terminar la operación dependiendo de si existe acarreo o no. Se ilustra con los siguientes ejemplos:
Ejemplo 15.- Sea A= (100)2. y B = (10)2 realizar A – B usando complemento a 1.
Solución: Los números binarios a operar se deben tener en con el mismo tamaño de palabra, es decir el mismo número de bits. Para este ejemplo se propone que la palabra sea de 4 bits.
Por lo tanto, A = 0100 y B = 0010, en seguida se obtiene el complemento a 1 del sustraendo, el cual se obtiene sustituyendo los 1 por 0 y los 0 por 1.
En este ejemplo se obtiene el complemento a 1 de B, que resulta ser 1101
Para hacer la resta, al minuendo A se le suma el complemento a 1 de B obteniendo suma parcial y a este valor, si existe acarreo, es decir solo si se excede el tamaño de la palabra en un bit “1”, se suma 1 a la suma parcial, obteniendo el resultado final.
A 0 1 0 0
Complemento a 1 de B + 1 1 0 1
1 0 0 10 1 excede el tamaño de la palabra
Se suma → + 1
A – B = 0 0 1 0
Comprobando en base 10
A = 0100 = 4 y B = 0010 = 2
A –B = 2
De aquí se puede generalizar como regla 1: cuando se realiza la resta de 2 números binarios usando complemento a 1, si existe acarreo en la suma parcial, este se suma a la suma parcial, y el resultado final es positivo.
Determinar la regla 2 a seguir cuando se restan dos números binarios usando complemento a 1 y en la suma parcial no existe acarreo.
Ejemplo 16.- Sea A= (100)2 y B = (10)2 realizar A – B usando complemento a 2.
Solución: Como ya se mencionó en el ejemplo anterior los números binarios a restar deben tener el mismo tamaño de palabra es decir el mismo número de bits.
Por tanto A = 0100 y B = 0010, enseguida se obtiene el complemento a 2 del sustraendo,
El cual se obtiene sumando en número 1, al complemento a uno:
en este ejemplo de B = 0 0 1 0
Complemento a 1 de B = 1 1 0 1
Sumar 1 + 1
1 1 1 0
Por lo que el complemento a 2 de B resulta ser 1110,
Para hacer la resta A-B, al minuendo A se le suma el complemento a 2 de B
A 10 1 0 0
complemento a 2 de B + 1 1 1 0
1 0 0 1 0
A – B = 0 0 1 0
De aquí se puede generalizar como regla 3: cuando se realiza la resta de 2 números binarios usando complemento a 2, si existe acarreo 1 en la suma parcial este se desecha, y el resultado es positivo.
Determinar la regla 4 a seguir cuando se restan dos números binarios usando complemento a 2 y en la suma parcial no existe acarreo.
Se recomienda hacer un resumen de las 4 reglas para la resta con números binarios.

