Los circuitos secuenciales se clasifican dentro de una categoría conocida como máquinas de estado, de la cual se distinguen comúnmente dos tipos:

• Máquina de Moore: Las salidas solo dependen del estado presente, las salidas del sistema son únicamente sincrónicas. Un ejemplo de este tipo de máquinas de estado son los contadores.

Figura 68. Máquina de estados de Moore

Máquina de Mealy: En esta máquina de estados las salidas se encuentran determinadas por el estado presente del sistema y por las entradas... El diagrama de bloques representativo de esta máquina se muestra en la figura 68 donde se observa que las salidas del sistema son tanto sincrónicas como asincrónicas.

Figura 69. Máquina de estados de Mealy

Se distinguen dos tipos circuitos secuenciales:

Síncronos y asíncronos

Los síncronos, requieren una señal de control procedente de un generador externo al propio circuito, que funciona, de modo que si no se aplica dicha señal no se hacen efectivos los valores presentes en las entradas. Este método se emplea cuando el sistema electrónico es complejo y los tiempos de conmutación de los diversos dispositivos que lo constituyen son distintos. La señal de control, también denominada reloj (CLK Pulse), se aplica a las entradas del mismo nombre de cada bloque integrado para sincronizar la transmisión de datos o información a través del sistema. La frecuencia de la señal eléctrica debe adaptarse a la velocidad de conmutación del dispositivo más lento del circuito.

En cambio, los sistemas secuenciales asíncronos no poseen entrada de reloj, y los cambios en las variables de estado interno y los valores de salida se producen al variar los valores de las entradas del circuito.

Diagramas de estado para máquina de Mealy

En estos apuntes se hará énfasis en las máquinas de Mealy, que son las más comúnmente empleadas en la solución de diseño para sistemas secuenciales. Todo ello sin dejar de reconocer la importancia de las máquinas de More.

Un diagrama de estados es una representación gráfica que indica la secuencia de los estados que se presentan en un circuito secuencial, teniendo en cuenta las entradas y salidas. El diagrama se forma con círculos y líneas. Los círculos representan los estados del circuito secuencial y cada uno de ellos contiene un número que identifica su estado. Las líneas indican las transiciones entre estados y se marcan con dos números separados por un (/), estos dos números corresponden a la entrada y salida presentes antes de la transición.

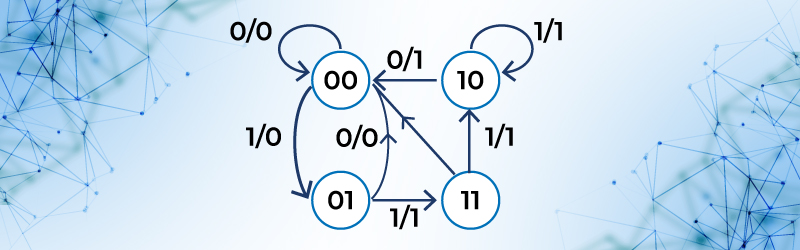
Figura 70. Diagrama de estados

Tablas de estado

Estado presente

Entradas

Estado siguiente

Salidas

Excitación.

Tabla 34. Tabla de estado

Las variables del estado presente más las de entrada definen el número de combinaciones posibles.

La tabla de estado para un circuito secuencial con m flip-flops y n entradas tiene 2m+n filas. El estado siguiente tiene m columnas, y el número de columnas depende del número de salidas.

Esto es para la tabla anterior:

Estados presentes, 2, (A y B) + 1 entrada X = 3 luego entonces se tienen 23 = 8 combinaciones posibles.

Las ecuaciones del circuito se establecen con los valores de las columnas de salidas y excitación que dependen del flip flop a emplear.

Es recomendable usar FF tipo D pues recordemos que su excitación se denomina espejo, es decir si entra un 0 la salida a estado siguiente será 0

4.4.1. Metodología para el diseño de sistemas secuenciales síncronos simples

Para la realización del diseño de un circuito secuencial es conveniente seguir los cuatro pasos siguientes:

1. Definición del problema.
2. Establecer el diagrama de estados que den solución al problema.
3. Construir Tabla de Verdad del diagrama propuesto y realizar la obtención y reducción de ecuaciones.
4. Dibujar el diagrama esquemático del circuito lógico que dé solución al problema.

1. Definición del problema. En este punto conviene definir y entender perfectamente el problema propuesto, para ello, como resultado final de este punto tendremos definidos.

Si existen valor inicial y valor final Es decir, si el circuito deberá iniciar en algún valor determinado o si también tendrá un valor en que termine la secuencia.

Número de entradas de control. Se refiere a que si el sistema tendrá señales de entrada que dependiendo de su valor modifiquen la secuencia que el circuito deberá ejecutar, es importante tener en cuenta que Una sola entrada tiene dos valores diferente es decir para la entrada única E1 se tendrá E1=0 y E1= 1. Para dos entradas E1 y E2 se tendrán 4 valores; 00, 01, 10, y 11

Número de Estados requerido. Se refiere a cuántos estados resuelven el problema propuesto.

Número de FF a emplear. Determinar el Número de FF necesario para generar los estados, se determina con la relación 2No de FF ≥ No de Estados. Por ejemplo para cuatro estados, será el No de FF = 2, pues 22 ≥4. Para 9 estados se requieren 4 FF, pues 24≥9.

Número de bits salidas. Es definir el número bits que permitirán tener la salida requerida. Por ejemplo para una secuencia que tenga como número mayor 111101 se requieren 6 bits de salida.

Determinar si será una máquina de estados tipo More o Mealy. Finalmente conviene definir con qué tipo de máquina de estados se propondrá la solución. Comentario: es posible emplear los dos tipos de máquina para resolver un mismo problema, el decidir cuál conviene, depende del contexto general de donde se desprende el problema a resolver. Ilustrarlo queda fuera del propósito de estos apuntes.

2. Establecer el diagrama de estados que dé solución al problema.

Dependiendo del tipo de máquina a emplear se propone una solución en diagrama de estados, se deberá verificar a detalle y cubriendo todas las posibilidades posibles que verdaderamente sea una solución al problema a resolver. Tener en cuenta que si se tienen por decir, 2 entradas de control, cada estado deberá tener cuatro posibles salidas, hacia el mismo u otro estado. Esto es n entradas da 2n salidas. También existen técnicas para reducir estados redundantes o repetidos, se recomienda ver los libros señalados en la bibliografía.

3.- Construir Tabla de Verdad del diagrama propuesto y realizar la reducción de ecuaciones.

A partir del diagrama de estados se obtiene la información para determinar la tabla de verdad, llenando los campos que se proponen.

En la figura se muestra una tabla de estados para 2 FF, FA y FB, con una entrada E1 con un solo bit de salida Y y empleando FF tipo D.

Tabla 35. Ejemplo de tabla de estados

Como ya se indicó anteriormente, debemos notar que las columnas de estado presente y entrada definen el tamaño de la tabla, para este ejemplo es 23 por tener 2 estados + 1 bit de salida.

Las ecuaciones que se buscan las definen las columnas de salidas Y y excitación DA y DB.

4.- Dibujar el diagrama esquemático del circuito lógico.

Se recomienda que en el dibujo esquemático, además de dibujar las compuertas con su símbolo, se indiquen los números correspondientes de la compuerta a utilizar.

El procedimiento de diseño se ilustra con los siguientes ejemplos:

Ejemplo 5.- Diseña un circuito contador que siga la secuencia… 0, 2, 4, 8,… no tiene entrada, no tiene valor inicial ni valor final. Empleando máquina de Moore.

Solución. Para este problema en particular en que se requiere generar la secuencia 0,2,4,8 en binario, tendremos:

¿Existen valor inicial y valor final?

R.- no existen

¿El número de entradas de control?

R.- no existen

¿Número de Estados requerido?

R.- se necesitan 4 estados, para generar cada uno de los valores de 0, 2, 4 y 8

Número de FF a emplear ( se tiene la siguiente ecuación: 2FF= Número de estados)

R.- se usarán 2 FF para generar los 4 estados necesarios.

Número de bits salidas

R.- Se definen X, Y, Z, y W como bits de salida. Para poder tener el mayor número 810 = (1 0 0 0)2

Determinar si será una máquina de estados tipo More o Mealy.

Para este ejemplo se propone usar una máquina tipo More, puesto que la salida está directamente relacionada con el estado.

2.- Diagrama de estados (maquina de Moore).

Figura 71. Diagrama de estados (maquina de Moore)

3.- Construir Tabla de Verdad del diagrama propuesto y realizar la reducción de ecuaciones.

Para este ejemplo la tabla de estados no contiene la columna de entradas por lo tanto el tamaño de la tabla será de 22.

Tabla 36. Tabla de verdad del ejemplo 4

Del diagrama se observa que del estado 00 se va al 01 y que su salida es 0000, del estado 01 se va al 10 con salida 0010, del 10 al 11 con 0100 de salida y finalmente del 11 se va al 00 con salida 1000. lo que se refleja en la tabla.

Finalmente en la columna de excitación se contempla el uso de FF tipo D por lo que para DA y DB se pondrán los valores de A y B de la columna del estado siguiente, pues recordemos que a los FF tipo D se les conoce también como de espejo.

Las ecuaciones que se buscan son

X = AB          Z = A’B

Y = AB’          W = 0

DA = A’B + AB’

DB = A’B’ + AB

Actividad complementaria 1:

---

Desarrolla la solución para este ejemplo usando máquina de Mealy.

Ejemplo 6.-Diseña circuito en donde si la entrada es 1 se muestra la secuencia: …8,4,2,1… y si la entrada es = 0 se muestre la secuencia … 1,2,4,8…empleando máquina de Mealy.

Solución

1. Definición del problema.

Si E= 1 entonces mostrar …8,4,2,1…

E= 0 entonces mostrar …1,2,4,8,…

No existe valor inicial ni valor final.

Número de entradas = 1 = E

Número de salidas = 4 = X, Y, Z, W

Número de estados = 4 por tanto el No de FF = 2 = A, B

Diagrama de estados (máquina de Mealy).

Figura 72. Diagrama de estados (máquina de Mealy)

Tabla 37. Tabla de verdad

Ecuaciones

X = ∑(3,6)

Y = ∑(2,4)

Z = ∑(2,7)

W = ∑(0,5

DA = ∑(1,2,4,7)

DB = B

Figura 73. Diagrama esquemático

Ejemplo 7.-Utilizando máquina de Mealy. Diseña el diagrama de estados de un circuito secuencial con una entrada W sincronizada a la señal de reloj, que acepte la secuencia 0011 y que cada vez que la detecte, su salida se Q ponga en ALTO y regrese a condiciones iniciales para detectar de nuevo la secuencia.

Solución

1. Definición del problema.

A como se van presentando los valores de 0 o 1 en la entrada W, se “generará” una secuencia de 0 y 1,( …00001100101110011011000100…), se desea detectar cuando ocurra 0011 poniendo en ALTO la salida Q y restableciendo las condiciones iniciales a fin de detectar nuevamente la ocurrencia de otra secuencia.

2.- Diagrama de estados

a).- máquina de Mealy, Diagrama de estados para el detector de secuencia 0011

Figura 74. Diagrama de estados para el detector de secuencia 0011

Ejemplo 8.-Empleando máquina de Moore, determina las ecuaciones para el circuito.

Solución

En el modelo de Moore Figura 74. la salida está en el mismo estado por eso se genera un estado más que en la máquina de Mealy, además de que después de detectar la secuencia correcta 0011 en E4, la entrada siguiente es considerada como el primer dato.

Figura 74. Diagrama de estados para el detector de secuencia 0011 (primer dato)

Tabla 38. Detector de la secuencia 0011 (máquina de Moore)

Las ecuaciones son:

Q= ∑(8,9)

DA= ∑(7)

DB= ∑(2,4,5,6)

DC= ∑(0,5,8)

Actividad complementaria 2:

---

Construye la Tabla de Verdad del diagrama propuesto y realiza la reducción de ecuaciones.

Las ecuaciones son:

Q = ABW ∑(7)

DA = A’BW’ + AB’W’ + AB’W = ∑(2,4,5)

DB = A’B’W’ + AB’W + ABW’= ∑(0,5,6)

Actividad complementaria 3:

---

Construye el diagrama esquemático del circuito.