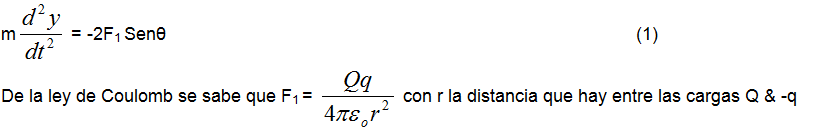Introducción. Definición.- La Electrostática es la parte del Electromagnetismo, que describe, analiza y cuantifica los fenómenos físicos relacionados con las micropartículas electrones y protones en reposo. A través del tiempo se ha encontrado que “todos” los materiales tienen este tipo de micropartículas; experimentalmente se observa que un material (objeto de plástico) al ser frotado (tallado ver figura siguiente) con algún lienzo, en dicho material se genera una propiedad física que inicialmente no tenía. |
|
La barra de plástico después de ser frotada se acerca a un pequeño pedazo de papel (5mm²) y la barra lo atrae cosa que inicialmente no la hacía. El mismo experimento se repite con una barra de vidrio y se frota con un paño de algodón con poliéster y adquiere una propiedad física Como un tercer experimento se colocan ambas barras de plástico y vidrio en péndulos electrostáticos cerca una de la otra y se observa una atracción entre ambas barras; como conclusión de esta observación en cada barra se generó una propiedad física que generó una fuerza de atracción mutua. |
Como un cuarto experimento, se frotan dos barras del mismo material y con el mismo lienzo y con ellas se hace el tercer experimento y se observa una fuerza de repulsión entre las barras participantes. Una conclusión de estas observaciones es que en cada barra se generó una propiedad física diferente; aclarando que macroscópicamente no se observa nada en los materiales participantes ( disminución o aumento de tamaño); sin embargo microscópicamente existe una pérdida o una ganancia de micropartículas, que por definición se les llamó electrones que son parte de los átomos que todos los materiales tienen, de tal forma que cuando una barra de plástico es frotada pierde electrones y queda con exceso de otras micropartículas llamadas protones. En el caso de los cristales estos quedan con exceso de electrones generándose dos barras con ganancia o pérdida de electrones, que por definición se concluyó que los materiales con exceso de protones se dice que están cargados positivamente (+) y los objetos con exceso de electrones se dice que están cargados negativamente (-). Por el tamaño de estas micropartículas algún objeto con electrones o protones se considera como una carga puntual; tales que de acuerdo a las observaciones experimentales se concluye:
|
y la de un protón es de .png){kind=small}
; con estas masas es saludable cuestionar el tamaño de dichas micropartículas; asimismo las unidades de carga se han definido como Coulombs; tales que para un protón se le asigno .png){kind=small}
y para el caso de un electrón una carga negativa de neg.png){kind=small}
.
representa a la carga puntual número uno, 
a la carga puntual número dos ó es un sistema de referencia inercial, 
el vector de posición que da la posición de la carga puntual uno, 
vector que indica la posición de la carga puntual dos, 
la fuerza que ejerce la carga puntual uno sobre la carga puntual dos; considerando que las dos cargas puntuales son del mismo signo y que el observador mira la carga puntual 
es la magnitud de 
indica la dirección de dicha fuerza, entonces: 
que las separa, disminuye la magnitud de la fuerza 
, en estas condiciones las cargas puntuales 
y 
; quedando la fuerza resultante como: 
y colocando el sistema de referencia en la esfera derecha como se muestra en la figura adjunta; con T la tención en la cuerda mg la fuerza que genera el campo gravitacional terrestre y Fe la fuerza electrostática producida por la carga q de cada esfera; quedando:
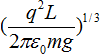
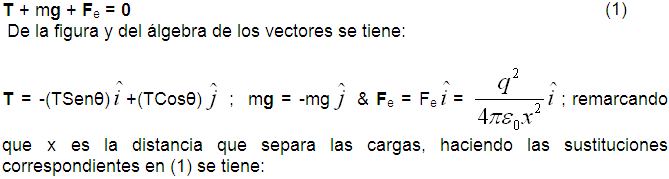
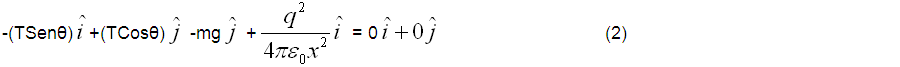
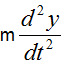; con m la masa de la carga (-q), por lo que:
